Отправитель ~

Передатчик U

\от4Лш>шл Н Передатчик

отпрйттель - Переватчик

Линий связи

Разделитель - npueMHuiPnoj,fi,

FS-1

Разделитель - Приемник - олуттель \

Рис. 4-2. Схема многоканальной связи.

Й

передатчиком и приемником. Технически это возможно осуществить лищь при использовании в качестве сигналов электрических колебаний сравнительно высоких частот (приблизительно от 10 гц до 10 Мгц).

Временное и спектральное представление сигнала

Носителем сигнала является некоторая физическая величина (ток, напряжение, напряженность электрического поля), изменяющаяся во времени. Поэтому для опи-

Рис. 4-3. Графическое изображение периодического сигнала.

Однако сигналы связи всегда ограничены во времени и поэтому не являются периодическими функциями времени. Например, одиночный сигнал (импульс) существует лищь в течение времени т. Такой сигнал можно рассматривать как предельный случай периодической последовательности импульсов длительностью т при неограни- ченно возрастающем периоде их повторения jTj -> с . При указанном предельном переходе частотный интервал Qj =

= -=г- между гармониками неограниченно сокращается, 1

а амплитуды гармоник уменьщаются. Таким образом, спектральным представлением непериодической функции является не дискретный ряд грамоник, а сумма бесконечно большого числа бесконечно близких по частоте колебаний с исчезающе малыми амплитудами. Спектр такой функции является сплошным, так как состоит из непрерывной последовательности частот. При графическом изображении такого спектра вдоль оси ординат откладывают не амплитуды составляющих (они бесконечно малы), а предел отношения амплитуды Л„ к полосе частот, отделяющей соседние спектральные линии. Этот предел называется спектральной плотностью амплитуд Ф (fi).

В качестве примеров на рис. 4-5 приведены спектры одиночного прямоугольного импульса ограниченной во времени последовательности прямоугольных импульсов, импульса в виде одного полупериода синусоиды и ограниченного во времени отрезка синусоиды.

Сравнивая спектр одиночного прямоугольного импульса со спектром периодической последовательности подобных импульсов, можно заметить, что огибающая сплошного спектра одиночного импульса и огибающая линейчатого спектра периодической последовательности таких же импульсов совпадают по форме. Это правило относится к импульсам любой формы.

сания сигнала могут быть использованы функции времени / (О или графики (рис. 4-3), выражающие изменение во времени той или иной физической величины.

Иногда более удобным является не временное, а спектральное представление сигнала. № математики известно, что периодическая функция времени с периодом повторения может быть представлена суммой синусоид с надлежащим образом подобранными амплитудами Afi и фазами ф„:

/ (О = 0 + 2 COS ( Gi/ ф„). п=1

Частоты этих синусоид (гармоник) кратны основной 2я

частоте = -=-, с которой повторяется во времени перио-i 1

дическая функция / (t).

Таким образом, если сигнал, подлежащий передаче, является периодическим, то он состоит из постоянной составляющей А^, первой гармоники А^ cos <Pi),

второй гармоники /4 2 cos (2Si-(-фг) и ДРУГих высших гармоник с частотами Зй, и т. д. Сумма всех этих гармонических составляющих равна сигналу и полностью описывает изменение сигнала во времени. Передача по каналу связи самого сигнала или всех его гармоник приводит к одинаковым результатам.

Совокупность амплитуд гармоник Л„ сигнала связи называется спектром сигнала. Графически спектр периодического сигнала изображается в виде вертикальных отрезков (спектральных линий), равноотстоящих друг от друга. Такой спектр называется линейчатым (рис. 4-4).

f(t)

\\A\~V\

Рис. 4-4.

О Si,2a)3£i,4£2, BSi,7iljBSi,3Sl, l1S?.j12%l3Si,14Slt

Zl£ 4lt 67Z

Г г r

Периодическая посчедовательность прямоугольных импульсов' и ее спектр.

Из рис. 4-4 и 4-5 видно, что огибающие спектров, начинаясь в области низких частот, уходят в область бесконечно больших частот. Но по мере роста частоты амплитуды составляющих и спектральные плотности уменьшаются, и, начиная с некоторой частоты, они вносят настолько малый вклад в общую сумму, что с ними можно не считаться. Таким образом, сигналы связи следует сЧй-

тать функциями с ограниченным спектром. Интервал частот, в котором размещается ограниченный спектр сигнала, называется шириной спектра.

При практической оценке ширины спектра импульса (в отсутствие особых требований к форме импульса) допускается отбрасывать высшие частотные составляющие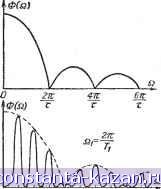

о п, гп, safici, 5а, би, 7s2, 8и, аз

0(S2)

О ill Za,3Si,4Si,Ssi,6Si,7Si, 8S},SSi

f(t)

о SI, га, 3i3, 4ii,

Рис. 4-5. Спектры непериодических сигналов.

а - одиночного прямоугольного импульса; б - ограниченной последовательности прямоуго.чьных импульсов; в - одиополу-периодного импу.чьса; г - отрезка синусоиды.

спектра, суммарная энергия которых не превышает 5-10% энергии импульса. При этом оказывается, что ширина F спектра импульсов практически любой формы определяется соотношением

т. е. произведение из длительности импульса на ширину его спектра есть постоянная величина порядка единицы.

Сокращая длительность импульса, мы во столько же раз увеличиваем ширину его спектра. В пределе при т -> О получаем f оо, т. е. импульс бесконечно малой длительности имеет бесконечно широкий равномерный спектр.

Ширина спектров реальных сигналов

При телеграфии буквы, цифры и знаки передаются с помощью кодов, образуемых путем комбинирования импульсов и пауз между ними. Например, при передаче сообщения по коду Морзе электрический сигнал вы-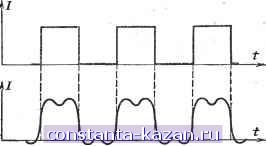

Рис. 4-6. Те.чеграфный сигнал в виде пос.чедовате.чьности точек и его форма при учете лишь трех гармоник.

ГЛЯДИТ как последовательность коротких (точки) и длинных (тире) прямоугольных импульсов, разделенных паузами, равными длительности коротких или длинных (между буквами) импульсов. Наиболее широкий спектр такой последовательности получается при передаче одних точек, разделенных короткими паузами. Чтобы отличить точку от паузы, достаточно сохранить в этом спектре лишь первые три гармоники (рис. 4-6).

Таким образом, ширина спектра телеграфного сигнала равна утроенной частоте следования точек, разделенных короткими паузами.

Частота при передаче 100 слов в минуту при среднем числе букв в слове, равном 6, и при среднем числе точек на букву, равном 10, будет:

100-6.10

--= 100 ец,

т. е. F = 300 гц.

Для передачи речи требуется воспроизведение частот в полосе 300-2 ООО гц. Поэтому в служебной (коммерческой) радиотелефонии используется полоса частот 300-2 400 гц.

Для очень хорошей передачи пения и музыки требуется полоса 30-15 000 гц. Звуковых колебаний с более высокими частотами человек не слышит. Но передача такого широкого спектра связана с большими техническими трудностями. Поэтому ограничиваются передачей более узких спектров, исходя из следующей примерной оценки качества звучания (табл. 4-2).

Таблица 4-2

В телевидении для точного воспроизведения движущегося изображения число строк должно быть достаточно велико. По стандарту, принятому в СССР, число строк равно 625. Такая яе четкость должна быть вдоль горизонтального размера кадра, в V3 раза превышающего вертикальный размер. Таким образом, кадр

625-4.625

г 500 ООО различных элементов.

состоит из

Наибольшую частоту получим в том случае, когда передается последовательность чередующихся черных и белых элементов. При развертывании по строкам такой последовательности на протяжении каждого кадра получается 250 ООО периодов, а в секунду передается 25 кадров. Следовательно, наибольшая основная частота телевизионного сигнала

/i к 250 000-25 X 6 Мгц.

Эту частоту принимают за верхнюю частоту спектра телевизионного сигнала. Нижней частотой спектра яв- ляется частота 50 гц, с которой следуют импульсы синхронизации.

Таким образом, спектры сигналов содержат сравнительно невысокие частоты. Непосредственная передача таких сигналов без проводов не может быть осуществлена из-за технических трудностей их излучения. Эффективного излучения и распространения электрических сигналов на дальние расстояния можно добиться лишь на высоких частотах. Поэтому перед поступлением в линию связи спектр сигнала должен быть передвинут в область высоких радиочастот. Это преобразование называется модуляцией.

Канал связи можно охарактеризовать также тремя величинами: 1) временем Т^, в течение которого канал выполняет свои функции; 2) полосой частот F, которую канал способен пропустить, и 3) полосой уровней Я,, зависящей от допустимых нагрузок аппаратуры канала. Произведение этих величин называют емкостью канала связи (рис. 4-7):

Передача сигнала по данному каналу связи возможна лишь в том случае, если основные характеристики сигнала не выходят за границы соответствующих характеристик канала. Если же этого не соблюдается, но объем сигнала не превышает емкости канала, то передача сигнала возможна лишь после согласования сигнала с каналом, которое заключается в преобразовании объема сигнала. Применяемые в радиосвязи преобразования объема сигнала и геометрические образы этих преобразований представлены в табл. 4-3. Указанные преобразования должны осуществляться без уменьшения объема сигнала или без потери заключенной в сигнале информации.

Если объем сигнала превышает емкость канала, то по этому каналу связи передача сигнала без потери информации невозможна.

Основные характеристики сигнала н канала связи

Подробное временное или спектральное описание сигнала не всегда бывает нужно. Достаточно полную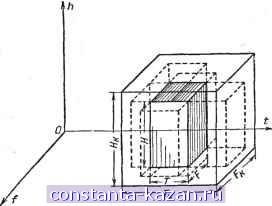

Рис. 4-7. Геометрические образы объема сигна.ча и емкости кана.11а.

характеристику общих свойств сигнала дает указание: 1) длительности сигнала Т; 2) ш и р и н ы спектра сигнала Р и 3) превышения сигнала над помехой

я = 1ое- ,

где Рс - средняя мощность сигнала; Рп - средняя мощность помехи.

Произведение этих величин называют объемом сигнала (рис. 4-7):

V = ТРИ.

* Эту характеристику называют также динамическим диапазоном или уровнем сигнала над помехой.

Модуляция

При любом виде связи передача сигналов осуществляется с помощью какого-либо физического переносчика. Переносчик должен обладать способностью хорошо распространяться по линии связи. В телеграфии и телефонии в качестве такого переносчика используется постоянный или импульсный электрический ток, а в радиосвязи - электромагнитная волна, способная распространяться без проводов на весьма значительные расстояния*.

Чтобы заложить информацию в переносчик, на передающей стороне осуществляется его модуляция, т. е, производится воздействие на тот или иной параметр переносчика (величину тока, частоту колебания и т. д.) в соответствии с передаваемым сообщением. В табл. 4-4 и 4-5 показаны используемые в связи виды модуляции; различия между ними определяются как выбором переносчика, так и выбором параметра переносчика, подвергающегося изменению (модуляции).

В радиосвязи основной смысл модуляции заключается в переносе спектра передаваемого сигнала из области низких частот в область высоких радиочастот.,

Например, если по радиоканалу передается сигнал на низкой частоте (один тон)

U-thU cos Qt,

то при амплитудной модуляции высокочастотного переносчика

и = и cos CO(f

в такт с передаваемым сигналом должна меняться амплитуда переносчика:

ллг = (С^о и cos Gj<) cos (0(1? =

= Ufj{l- т cos QJ) cos (u(< = cos (nt

mUf, cos (nt cos Qt = l/o cos co f -1 X

X cos (и„ -f Q) -f COS ( 0 - fi J t.