Переносчин

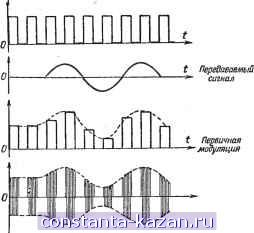t Вторичная

Рнс. 4-9. Амплитудная модуляция высокочастотного колебания модулированной последовательностью импульсов.

частота, фаза и длительность импульсов. В соответствии с этим различают амплитудно-импульсную, частотно-импульсную, фазово-импульсную модуляции и модуляцию импульсов по длительности. Модулированная последовательность импульсов может передаваться по проводам. Ширина спектра при этом определяется длительностью импульса т (см. табл. 4-5).

Но модулированная последовательность импульсов может использоваться и в радиосвязи для вторичной модуляции высокочастотного переносчика (рис. 4-9). В этом случае спектр последовательности импульсов сдвигается в область высоких радиочастот.

Дискретные и непрерывные сообщения

Все сообщения, передаваемые по радиоканалам, можно разделить на две группы: дискретные сообщения и непрерывные сообщения. В дискретном сообщении передаче подлежат отдельные знаки, буквы. Примером дискретного сообщения является текст. В непрерывном сообщении передаются непрерывные функции времени (например, звук при передаче музыки или речи).

Кодирование дискретного сообщения

Передача дискретного сообщения сводится к передаче чисел. Например, все буквы алфавита (а также цифры и- знаки препинания) можно занумеровать и передавать по каналу связи соответствующую последовательность чисел. Конечно, полиции связи передаются не сами числа, а соответствующие им посылки: импульсы различной амплитуды или длительности. Эти посылки называются элементами кода.

Если число т элементов кода (основание кода) равно числу знаков алфавита, то при передаче сообщения каждый знак передается одним элементом кода, а общее число п элементов сигнала равно числу передаваемых знаков. Такой способ кодирования энергетически невыгоден. Он требует значительных мощностей, чтобы в условиях помех отличать большое количество элементов кода друг от друга, так как различие между элементами кода должно быть больше величины помехи.

Поэтому для связи выгодней использовать коды, у которых число элементов (r.i) значительно меньше, чем число, знаков алфавита. Каждый знак алфавита пере-

дается не одним элементом кода, а определенной комбинацией из элементов кода, число элементов сообщения (и) возрастает, но превышение сигнала над помехой может быть снижено.

Особенно выгоден код, состоящий из двух элементов (двоичный код). Одним элементом этого кода может быть посылка тока, несколько превышающая помеху, а другим - отсутствие посылки. Мощность сигнала в этом случае должна превышать мощрюсть помехи лишь настолько, чтобы можно было отличать наличие посылки от ее отсутствия.

В качестве примера на рис. 4-10 выбран алфавит, состоящий из шести первых букв русского алфавита - А Б В Г Д Е, составлено слово В Е Г А и осуществлено кодирование этого слова в шестиэлементном и двухэлементном (двоичном) кодах. В первом случае каждый знак

Ь В Г Д Е

г 3 4 5 е

3 611

а) т=В

А 6 В

1 г 3

001 010 он

г Д

100 101

Е

в

в £ г А

3 6 11 01 1 1 1 0 10 0 0 01

Л1л.Л 1т: пл п: Г1 in m

б) т=г

n=l2

Рнс. 4-10. Кодирование дискретного сообщения при шести элементах кода (а) и при двух элементах кода (6).

алфавита передается одним элементом, сигнал содержит и = 4 элемента, а число уровней передаваемого сигнала равно шести. Во втором случае каждый знак алфавита передается трехзначной комбинацией из двух элементов кода, число элементов сигнала возрастает до п = 12, но зато число уровней сигнала сокращается до двух.

Кодирование непрерывного сообщения

Передача непрерывных сообщений также сводится к передаче последовательности дискретных чисел. Непрерывные функции времени, передаваемые по каналам связи, всегда обладают ограниченной шириной спектра F. Для передачи функции / (t) с ограниченным спектром не нужно передавать все значения функции, достаточно передать лишь отдельные мгновенные значения ее (рис. 4-11), отсчитанные через интервалы времени

2Р

Таким образом, функция конечной длительности Т с ограниченным спектром F определяется отдельными значениями, число которых равно:

Т

Если эти значения переданы по каналу связи, то по нин на приемном конце исходная функция с ограниченным спектром может быть восстановлена единственным образом.

Это положение, известное в теории связи как теорема Котельникова, показывает, что между передачами дискретного и непрерывного сообщений приниципиальной разницы нет. В обоих случаях дело сводится к передаче отдель-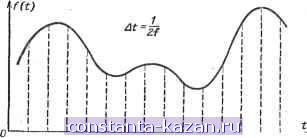

гм ж Ш 5М 6М 7М But But ЮМ 1Ш ШШ 1Ш

I !

I I

I I I

I !

значение функции /(О одним импульсом величиной

/6 (г= 1, 2, 3.....т). При этом полное число элементов

(импульсов) в сигнале длительностью Т будет:

Однако выгодней передавать значения непрерывной функции кодом с меньшим основанием т. В этом случае каждое значение функции передается не одним элементом кода, а определенной комбинацией из элементов кода. Следовательно, число п элементов сигнала возрастает, но число необходимых уровней mt уменьшается, что влечет энергетический выигрыш.

Наиболее выгодной является передача непрерывного сообщения при помощи двоичного кода. Этот случай называется кодов о-и мпульсной модуляцией (рис. 4-13).

Нужно отметить, что передача непрерывной функции двоичным кодом может вестись при любом виде модуляции (АИМ, ДИМ, ЧИМ и ФИМ). Поэтому, несмотря на название, кодово-импульсную модуляцию следует рассматривать не как самостоятельный вид модуляции, а как применение низшего кода при том или ином виде модуляции.

Рис. 4-П. к теореме Кстельннкова-

ных значении, которые могут быть занумерованы и закодированы.

При кодировании этих значений имеет смысл различать только те значения функции f (t),> разность б между которыми вдвое превосходит максимальное значение помехи акс:

S > 2иакс-

В противном случае помеха, накладываясь на сигнал, будет переводить одно значение в другое и на приемном конце не удастся отделить помеху от сигнала (рис. 4-12)

Таким образом, если максимальное значе- о ние непрерывной функции t/иакс. то она должна передаваться при числе различных уровней

т - -i-

Число возможных сообщений

Пусть передача информации осуществляется кодом, содержащим т элементов. Передавая первый элемент сигнала, мы осуществляем выбор из т элементов кода, т. е. таким способом можно передать т различных сообщений. Передавая второй элемент сигнала, мы снова осуществляем выбор из т элементов кода, но число возможных комбинаций элементов кода в первых двух элементах сигнала равно rr?. Значит, двумя элементами сигнала можно передать rr? различных сообщений. Три элемента сигнала позволяют передать rrfi различных сообщений и т. д.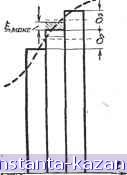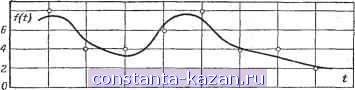

0100

\01 а о

\010 о

о 10 о

0 010

Рис. 4-12. Квантование сигнала.

Выбор конечного числа m уровней для передачи непрерывной функции времени называется квантованием.

Считая эти уровни элементами кода, т. е. взяв число т за основание кода, мы можем передать каждое

Рис. 4-13. Кодово-импульсная модуляция.

В общем случае число возможных сообщений, которое может быть передано сигналом из п элементов при коде, содержащем т элементов, равно:

Например, в системе Бодо каждая буква алфавита передается комбинацией из пяти положительных или отрицательных посылок тока одинаковой величины. Поскольку здесь т=2ип=5, тос помощью такой системы могут быть переданы т = 2 = 32 буквы.

В качестве второго примера рассмотрим передачу непрерывной функции времени. Пусть используемое для

/3t=-jg сек

Рис. 4-14. Непрерывная (пунктир) и квантованная функции времени (таких кривых можно провести Ю'о шт.).

передачи число уровней сигнала равно 10, ширина спектра передаваемых сигналов не превышает 5 гц, а длительность сигнала равна 1 сек. Какое число различных функций времени может быть передано в этих условиях?

Т

Здесь пг = 10, а число элементов сигнала .= д^ =

= 2FT = 2 5 = 10. Следовательно, число возможных сообщений

N=171 -= 104

Это число выражает количество различных ступенчатых (квантованных) кривых, которые могли бы быть проведены на рис. 4-14.

Таким образом, основание кода т и число элементов в сигнале п определяют число возможных сообщений Л' при передаче как дискретных, так и непрерывных сообщений.

Количество информации

Передача сообщений всегда связана с выбором данного сообщения из всех других возможных сообщений. Чем больше число возможных сообщений, из которых выбрано передаваемое сообщение, тем более подробную информацию оно несет. Например, два человека могут сообщить друг другу тем большую информацию, чем больше их общий словарный запас. Люди, говорящие на различных языках, испытывают затруднения в передаче

информащж друг другу.

аким образо.м, число Л' возможных сообщений может служить мерой количества информации, которое несет данное сообщение, так как это число показывает, из скольких возможных сообщений выбрано данное сообщение.

Однако само по себе число Л' неудобно для характеристики количества информации, так как не выражает пропорциональности между количеством информации и числом элементов сигнала п и, кроме того, зачастую приводит к чрезвычайно большим значениям.

Поэтому принято количество информации / измерять логарифмом числа возможных сообщений Л':

/ = logN = log2/ra = n logam.

Основание логарифма, равное двум, выбрано для того, чтобы наименьшее количество информации, получаемое от одного элемента (и = 1) при двоичном коде (т = 2), считать за единицу. Таким образом, количество информации измеряется в двоичных единицах.

Количество информации на один элемент сигнала

/ = = logjm

называется содержательностью сообщения. В зарубежной литературе эту величину называют энтропией.

Количество информации, переносимое сигналом, можно выразить через основные характеристики сигнала. Пусть на вход приемного устройства действует смесь сигнала и помехи. Будем считать, что присутствие сигнала может быть замечено, если действующее значение этой смеси превысит действующее значение помехи. Тогда число различных уровней

Если ширина спектра сигнала F, то число элементов в сигнале

п = 2FT,

Следовательно,

/ = и logm = 2FT logj/i

/ = FT log2

Количество информации, передаваемое в системе связи за единицу времени,-

C = -=flog2 1 + -

называется пропускной способностью системы (или скоростью передачи информации).

Например, пропускная способность телеграфного канала, рассчитанного на передачу сигнала при F = = 300 гц и m = 2, составляет:

С= 2F log2/ra = 600 log2 2 = 600 дв. ед/сек.

Вероятностные характеристики сигнала

Если на передающей стороне сигнал можно предста- влять некоторой функцией времени / (О (близкой к периодической функции), то с точки зрения получателя -faKoe представление не соответствует истинному положению вещей.

Действительно, отправитель (или обслуживающие его лица) очень много знает о передаваемом сигнале, так как в его распоряжении находится й сообщение и код, преобразующий сообщение в сигнал. Он может до передачи записать сигнал и, таким образом, наперед знать каждое его значение. Он может по своему усмотре-

* Сигнал и помехи считаем независимыми, поэтому их средние мощности можно складывать.