жая числители и знаменатели в формуле (20-5), приходим к выражению дифференциального уравнения (20-4) в символической форме, где D - символ дифференцирования.

Переходная характеристика

Переходной характеристикой называют зависимость выходной величины от времени при условии, что на вход динамического звена в момент t = О подается ступенчатый сигнал (или сигнал включения) единичной- амплитуды. Переходная характеристика H{t) представляет реакцию системы на единичный сигнал включения. Практически Я(0

(Vj < Ce/j И (со)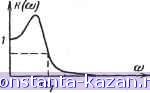

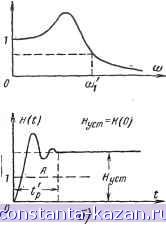ничейном участке изменения входной величины, где зависимость у т X является линейной. (рис. 20-П).

В случае, когда рабочая точка d лежит на криволинейном участке, реальную зависимость для малых отклонений от точки- d заменяют отрезком прямой, касательной в точке d. Коэффициент передачи при этом будет равен Кй = tg а. Такая замена называется линеаризацией характеристики реального звена.

Пример 1, Управитель частоты в- системе АПЧ (стр. 458). Зависимость между частотой гетеродина и управляющим напряжением

А/г = KyAuy.

Передаточная характеристика (коэффициент передачи)

Рис. 20-10. Иллюстрации положения: чем шнре частотная харак- теристнка, тем кратковременнее переходный процесс.

Амплитудно-частотная характеристика К (со) для случая (а) шире, чем для случая (б), поскольку при определенном уровне

К (со) < ю^; соответственно время установления (р окончательного значения переходной характеристики Я \t) (т. е. длительность переходного процесса) в случае (с) меньше, чем в случае (б); А - входной сигнал (ступенчатый сигнал единичной амплитуды).

для сложных систем находится без решения дифференциального уравнения простыми методами, основанными на связи между переходными и частотными характеристиками (стр. 446). Одно из положений, отражающих эту связь, говорит отом, что чем шире частотная характеристика (больше полоса пропускания), тем скорее протекают переходные процессы, т. е. тем быстрее устанавливается окончательная величина Я(0 (рис. 20-10).

2. Основные динамические звенья и их свойства

Ниже дается определение основных линейных дина-мческих звеньев и рассматриваются их характеристики.

Усилительное (или пропорциональное) звено

Это звено характеризуется постоянным (вообще говоря-, размерным) коэффициентом передачи К = . Сюда

относятся не только усилители, но и такие звенья, в которых одна физическая величина преобразуется в другую в постоянном отношении, В реальных условиях величина К является постоянной только на некотором огра-

Рис. 20-11. Характеристика усилительного (пропорционального) звена. На участке

у

аЬ отношение К = (коэффициент передачи звена)- постоянно.

на участке аЬ есть постоянная величина с размерностью гц/е.

Пример 2. Частотный дискриминатор в системе автоподстройки частоты (если не принимать во внимание инерционности выходных /?С-элементов) характеризуется зависимостью Ид = KpAf, где Ид - выходное напряжение; А/ - расстройка частоты f относительно переходной частоты дискриминатора (см. стр. 454). Передаточная

функция (коэффициент передачи) W = - = ~ = /Сд

на участке аЬ - постоянная величина с размерностью е/гц.

Инерционное звено

Инерционное звено описывается передаточной функ-

>- x{t) -ГО+1

Параметры звена:

Т - постоянная времени (с размерностью сек), характеризующая инерционность звена; К - коэффициент передачи звена (вообще размерная величина).

В установившемся режиме при постоянном входном -сигнале х = Xq производная выходной величины равна нулю; следовательно, полагая D = О, находим:

W (0) = к.

или уо = КХд (индекс нуль является обозначением установившегося режима).

Пример 1. Фильтр RC

6х 0-

т

Рис. 20-12. Фильтр RC нижних частот - пример инерционного звена.

Нижних частот (рис. 20-12). При синусоидальном вхоД-ном сигнале С/вх(/< )

hR + Xc) =

= ( + 7) = -

Но 1/вых=/Хс = /С0С

Обозначая

Отношение

где Т = i?C.

Заменяя /ш на D, получаем передаточную функцию

Точно такой же результат получается, если записать закон Ома для цепи, в которой символическое со- gj

противление емкости равно -.

Ra+Ri и заменяя /ш на D, найдем: IF (D) =

Ra + Ri

К

rjji-1

y(t)

= г + -j , но ВЫХ =c5 СДивых-

Следовательно, вх = {CRD + 1) вых и Ивых() 1

Пример 2. Реостатный усилитель с учетом выходной емкости лампы и входной емкости следующего Vj? каскада Сп (рис. 20-13). 2

Используя эквивалентную схему (рис. 2-13, б), можно записать:

где

г/выхаш) = 5:;вх(/со)-з7-,

к = к,- + + Кс = + - -f /шСп;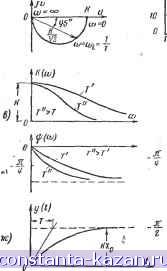

\Декада -Ленава

uebix (jw) = tBX (/w)

= f>EX (/w)

SRaRi

Ra + Ri + jaCnRaRl SRiRa 1

a + Ri CnRaRi

Ra+Ri

Рис. 20-14. Характеристики инерционного звена.

а - изображение звена на схемах; б - амплитудно-фазовая характеристика; в - амплитудно-частотная характеристика для двух звеньев с различными постоянными времени Т к Т'; г фазо-частотная характеристика для звеньев с постоянными времени Т' и Т ; д - логарифмическая амплитудная характеристика для К = 20 и Т= 0,06 сек; е>-.= у-: е-логарифмическая .фазовая характеристика ф,- (-1, построенная

в масштабе и/ю^-, где = --частота сопряжения (на ча-

Ф(ш^-) = 45°);

стоте сопряжения © = й>;

характеристика

ж - переходная t

здесь у U) = КХо (1 - е

Характеристики (рис. 20-14) Комплексный коэффициент передачи

к

= /С(со)е^<Р<>

Рис. 20-13. Реостатный усилительный каскад с учетом емкости и его эквивалентная схема. Представляется инерционным звеном.

/шГ -f 1

получается заменой D на /оз в передаточной функции. Амплитудно-фазовая характеристика К (Ja) = и{(о)+ jv (со).

Г

внутренняя проводимость лампы; Yq

где и (со) =

К

с (со) = -

Т+1 ~

суммарная емкостная проводимость; Уд= мость анодной нагрузки.

проводи-

1 + ш^Г^

окружность, расположенная в четвертом квадранте, пересекающая ось ь при со = О в точке с абсциссой К и стремящаяся к нулю при со со.

Амплитудно-частотная характеристика К

При <в = О К{а>) имеет максимальное значение, равное К. и убывает, стремясь к нулю с увеличением со. Чем больше Т, тем интенсивнее убывает /С(со) с ростом частоты

Фазо-частотная характеристика

г;((й)

Ф (со) = arc i

= - arc tg соГ.

При ш = О фазовый сдвиг равен 0. С увеличением частоты сдвиг по фазе выходных колебаний растет тем интенсивнее,

чем больше Т, стремясь к-- при со -> оо. На частоте СО/ = фазовый сдвиг составляет-- .

Логарифмическая амплитудная характеристика (ЛАХ).

По определению

L (со) = 20 lg 1(/ш) 1 = 20 lg/С (СО) = К

V1 + (соГ)

= 20Ig

= 20Ig/C -201gl/ l-f cori .

Для со используется логарифмический масштаб. Практически значительно удобнее пользоваться приближенными ЛАХ. Для очень низких частот ш С со/ = в подкоренном выражении величиной соГ можно пренебречь по сравнению с единицей и

L (со) г 20 Ig К - 20 lg 1 = 20 lg К

Для низких частот ЛАХ представляет горизонтальную прямую на уровне 20 lg К- Для высоких частот со > со/ =

= в подкоренном выражении можно пренебречь единицей. Тогда

Ц(л) 20 lg К - 20 lg юГ.

Выражение 20 Ig соГ = 20 lg со + 20 lg Г в логарифмическом масштабе представляет прямую, пересекающую ось абсцисс в точке а = coj, поскольку 20Ig со/Г = 20 lg I = 0. Ординаты этой прямой при увеличении частоты в 2 раза (от со до 2(й') возрастают на

AL2 = 20 Ig 2соГ20 lg соГ = 20 Ig 2 = 6 дб.

а при увеличении частоты в 10 раз (от со до Юсо') - на

ALjo = 20 lg Юсо'Г - 20 lg соГ = 20 ig 10 = 20 дб.

Это выражают словами: наклон прямой равен 6 дб на октаву или 20 дб на декаду. Ясно, что прямая - 20 Ig шГ также пересечет ось абсцисс в точке со = со но будет иметь наклон - 6 56 на октаву или - 20 дб на декаду.

Таким образом, точную ЛАХ можно заменить при- ближенной, состоящей из двух отрезков: горизонтального- до частоты со = W( и наклонного (с наклоном - 20 дб на декаду, выходящего из точки .4, имеющей абсциссу со/.

Частота (oi = ~ излома приближенной ЛАХ называется частотой сопряжения. Точная ЛАХ идет ниже приближенной (пунктирная линия- на рис. 20-14, д). Максимальная ошибка имеет место на частоте сопряжения и составляет величину, равную

Практически всегда пользуются приближенной ЛАХ, поскольку она строится чрезвычайно просто и мало отличается от истинной.

Логарифмическая фазовая характеристика может рассчитываться по стандартному графику (рис. 20-14, е). На

частоте сопряжения фазовый сдвиг составляет--- ,

поскольку

)=-arctg = -.

Переходная характеристика - экспонента с постоянной времени

l = KXo{l-e

Установившегося значения KXf, выходная величина достигает через 2,5-3 постоянных времени; следовательно, время регулирования

/р = (2,5 ч- 3)Т. Звено второго порядка

Звено описывается передаточной функцией

y(t) К

W (D) =

X (t) TD + %TD + I

(20-7)

Параметры звена:

К - коэффициент передачи, т. е. отношение выхдд-ной величины ко входной в установившемся режиме (при D = 0); Т - постоянная времени звена (размерность сек); - коэффициент затухания (безразмерная величина); при t, < 1 - процессы носят колебательный характер, а при S > 1 - апериодический характер. Пример 1. Последовательный контур LCR (стр. 422). Для преобразования передаточной функции контура к виду (20-7) необходимо ввести следующие обозначения:

LC = T = , т. е.Т= - (не путать Т с периодом

собственных колебаний 4 = 2л;Г), где соц - угловая частота собственных колебаний;

CR = 2t,T

CR. R 1

: -gjr = -g = --относительный коэффициент

затухания;

где

Тогда

W(D) =

характеристическое сопроти- вление контура; добротность.

Постоянная времени контура т выражается следующим образом: ,

1 Z

А = 20 lg (согГ)2 = 3 дб.

где а = -f- - коэффициент затухания.