Поскольку операция сложения выполняется значительно проще операции умножения, для определения свойств системы последовательно соединенных звеньев на практике чаще всего пользуются ЛАХ.

Пример 1. Последовательное соединение двух инерционных звеньев (рнс. 20-22, е и г).

Встречно-параллельное соединение (обратная связь)

Звено Wo. с находится по отношению к звену W во встречно-параллельном соединении (т. е. звено W охвачено обратной связью Wq. с), если вход звена Wo. с соединен с выходом звена W, а выходная величина г/с. с(0 звена Wo. с суммируется со входным воздействием x{t) или вычитается из него (рис. 20-24).

Передаточная характеристика эквивалентного звена К

ЛАХ. Наносятся две частоты сопряжения: щ =

и (02 = -TfT-. ЛАХ представляется: до частоты Oj -

прямой, параллельной оси абсцисс на уровне -f 20 lg К; между CDj и CD2 - прямой с наклоном - 20 дб/дек; выгНе (02 - прямой с наклоном - 40 дб/дек (предполагается Ше > (О,) ЛФХ. Складываются две фазовые характеристики с соответствующим пересчетом масштаба по оси абсцисс. Общий фазовый сдвиг при (о О равен нулю, при (D оо равен -п.

Амплитудно-фазоваяхарактеристика{см.рис.20-16,6).

Пример 2. Последовательное соединение интегрирующего и инерционного звена:

-А- W, = -

TD+l

К

D{TD-j-l)

Усе

0.С

Такой передаточной функцией описывается электрический серводвигатель (см. стр. 428).

Параллельное соединение (рис. 20-23)

В параллельно соединенных звеньях входной сигнал общий, а выходной сигнал является суммой выходных сигналов отдельных звеньев.

Рис. 20-23. Параллельное соединение звеньев:

= -ь vy. -Ь . . . -f-vy .

Передаточная функция W системы из и параллельно соединенных звеньев W], Wj, . . ., W равен сумме передаточных функций отдельных звеньев:

W=Wi-bW,-h...-bW = ,

где г = ; 2=f; п

Рис. 20-24. Соединение обратной связи (встречио-параллельиое соедияенне).

а - общее обозначение: б - обозначение отрицательной обратной связи и эквивалентное звено; в - следящая система с обратной связью; W - передаточная функция разомкнутой системы; Ф - замкнутой системы; х = - заданное значение регулируемой величины; у = вых ~ Действительное значение регулируемой величины (выход); Z = 6 = в^ых ~ вх ~ рассогласование.

Положительная обратная связь - на звено W подается сумма x(t) и г/о.с(0 так, что входной сигнал для Нравен:

z=-x(t) + yo.(t).

Отрицательная обратная связь - на звено IF поступает разность x{t) и у о. с(<), так что входной сигнал для W

. г= x{t)-~yo.{i).

В автома-йше наиболее часто (почти исключительно) используются отрицательные обратные связи.

Звено W, охваченное отрицательной обратной связью с передаточной функцией Wq. с. эквивалентно одному звену с передаточной функцией

У it)

x{t) 1-bWWo.c

Если Wo. с не зависит от D, то обратная связь называется жесткой.

При положительной обратной связи перед вторым членом знаменателя будет иметь место знак минус.

Частный случай: Wo. с = Ь Для которого

Ф =--

1 + W

соответствует охвату звена W отрицательной обратной связью, когда на сравнивающий элемент поступает выход-

ная величина ii{t), т. е. У(у,с = у. К такой схеме приводится усилитель с отрицательной обратной связью (рис. 20-26).

обычно следящая система. Для следящей системы х

у = ввых; г = е = ввх - бвых-Зависимостью

Для него (см. стр. 424) -

К

1 + W

где К =

определяется передаточная функция замкнутой системы Ф по передаточной функции разомкнутой системы W.

Пример 1. Инерционное звено с жесткой обратной связью (рис. 20-25).

Ri + Ra

и TD-\-\ RiRa

Ri + Ra -

v/(n)

(при условии, что i?2 > Ra)-Для пентода Ri Ra, К = SRa,

~ 1 -Ь SRa

1 + 2

RaPn

1 + SRa

. a]

Рис. 20-25. Инерционное звено с жесткой обратной связью. а - структурная схема; б - эквивалентное ннерцноиное звено.

Передаточная функция инерционного звена без обратной связи (разомкнутой системы)

К

1 +SRa

I; Т-э =

1 +SRa

Пример 2. Интегрирующее звено с жесткой обратной связью.

W =

Ввых(о Cbxw

№-f Г

= 5-: Wo.c =

- = р.

К

Для жесткой обратной связи передаточная функция яв- kjl.- тэ =

ляется действительным числом Р и

Wo.c=-j = p Ввых

(как правило О < Р < 1).

Передаточная функция звена с обратной связью (замкнутой системы)

%ых(0 W Кэ

рк

W

ввх (о ~ 1 + Wo.c ~TsD+l-

где /Сэ- J p , .э- 1 +

В результате охвата инерционного звена жесткой обратной связью образуется также инерционное звено с меньшим коэффициентом передачи Кэ <К и (что наиболее существенно) с меньшей постоянной

Тэ < Т. В частном случае при Р = 1

К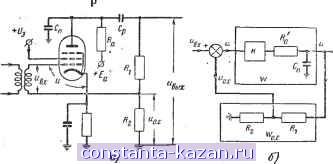

вкх

Рис.20-26. Усилитель с обратной связью.

а - принципиальная схема; б - структурная схема - эквивалентное инерционное звено W с обратной связью через сопротивления

/Сэ =

1 + К'

при > 1

/<э 1; Тэ =

К

Интегрирующее звено в результате рхвата жесткой обратной связью преобразуется в инерционное звено? Соответственно переходная характеристика преобразуется в экспоненту с постоянной времени Тэ, стремящейся к уровню /Сэввх-

Если Р = 1, то коэффициент передачи Кэ равен единице (выходная величина в установившемся режиме повторяет входную), а постоянная времени есть величина, обратная коэффициенту усиления,

Кэ - Г. Тэ = -j -

Для уменьшения инерционности звено можно охватить жесткой обратной связью. Постоянная времени уменьшается тем больше, чем выше К- Соответственно при большом К общий коэффициент передачи бущет близким к еди- Примером указанногр соединения может служить нице. Примером из области радиотехники может служить исполнительный двигатель (при Гдв = 0) с потенциометром

отрицательной обратной связи (рис. 20-27). Управляющая обмсяка двухфазного асинхронного двигателя питается Cft лампового усилителя переменного тока. С ротором двигателя связан потенциометр обратной связи, напряжение которого о. с вычитается из входного переменного напряжения и^х-

При наличии напряжения и на сетке лампы якорь двигателя начинает вращаться, перемещая связанный с ним через редуктор движок потенциометра обратной

Управляющая обмотка 0 +fa 0 двигателя

~1-1/ /Ь°в\ г !

(ЧООги)

обмотка двигателя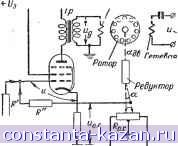

is R,R .R>Rac . I

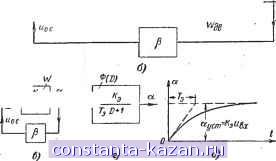Рис. 20-27. Простейшая следящая система с двигателем. а - упрощенная схема следящей системы для отработки угла а, пропорционального входному напряжению и^ б - структурная схема системы, /С^ - коэффициент передачи

входной цепи (от входа до сетки лампы); К^=--коэффици-

ент передачи лампового

усилителя и трансформатора; К^д=

[1/в-сек] - коэффициент передачи двигателя; Кр =

- в/град ] -

уст

- коэффициент передачи редуктора; Р =

коэффициент передачи цепи обратной связи; е - преобразованная структурная схема, К = Ki Kj KgKp; г - эквивалентная структурная схема (инерционное звено), К„ = -3-.: 7 = -

д - переходная характеристика системы.

К

связи Rfj. с. Возникающее напряжение о. с- пропорциональное смещению движка а и углу поворота якоря двигателя Одв противофазно входному напряжению, т. е. вычитается из него. Последнее достигается соответствующим выбором направления смещения движка.

Напряжение на сетке лампы пропорционально разности ывх и Ыо. с- так как и = /С](ывх- о.с)- Для R = = R = R Kj = 0,5 и = 0,5 (ыех- о-с)- Напряжение на управляющей обмотке у = Кгч, где коэффициентом Ks учитывается усиление лампы и наличие трансфор-

матора Тр. Угловая скорость вращения якоря двигателя пропорциональна напряжению Uy, Шдв = /Сдв у- Соответственно передаточная функция двигателя 1Гдв г -~- -

= Дв D

Угол поворота движка потенциометра а == КрИдв и напряжение, снимаемое с движка потенциометра, о. с - = Родв. Соответственно структурная схема в рассматриваемом примере состоит из интегрирующего звена, усилительных (пропорциональных) звеньев и цепн обратной связи р. Вся система эквивалентна одному инерционному

звену с коэффициентом передачи Кэ= к постоянной

времени Тэ = -щ. Коэффициент Кэ {град/е) характеризует

угол поворота движка потенциометра на единицу входного напряжения. Приведенный пример иллюстрирует следящую систему, предназначенную для поворота выходного вала (движок потенциометра) пропорционально входному напряжению. Инерционность системы характеризуется величиной Ts и зависит от Р и /С. Для уменьшения инерционности следует увеличивать коэффициент усиления.

Пример 3. Инерционное звено с дифференцирующим звеном в цепи обратной связи (рис. 20-28).

Рис. 20-28. Инерционное звено с дифференцирующим звеном в цепи обратной связи.

а - исходная структурная схема; б - эквивалентная структурная схема.

Передаточные функции звеньев равны соответственно: евых(0 К .

W (£>) =

Го.с(0) =

)(<)

во. с (О

TD-f 1

ввйхИ ГдО-Ы Передаточная функция системы

ввых /С(ГдР+1)

Ф(0) =

ввх (ГО-Ь 1)(ГдО-Ь l)-f/СГдО

/С(ГдО+1)

rr D2 + (Ti -Ь Тд -Ь /СГд) D -Ы

Соединение эквивалентно последовательному соединению двух звеньев: идеального форсирующего с коэффициентом передачи К и звена второго порядка. Таким соединением пользуются, если необходимо ввести в закон регулирования производную. Коэффициент передачи при этом не меняется, однако порядок системы увеличивается на единицу (вместо первого становится второй).

ЛАХ и ЛФХ замкнутой следящей системы

ЛАХ и ЛФХ замкнутой системы строится по ЛАХ и ЛФХ разомкнутой системы с помощью номограмм (рнс. 20-29): вычисленных на основе зависимости

1-f W