§ 20-3]

Устойчивость систем автоматического регулирования

20-3. УСТОЙЧИВОСТЬ СИСТЕМ АВТрМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Система автоматического регулирования может выполнять свои функции, если она устойчива. Это необходимое условие, работоспособности системы..

Анализ устойчивости производится путем исследования математических уравнений, описывающих поведение системы. Поэтому должно быть сформулировано математическое определение устойчивости, пригодное для анализа уравнений. Наиболее удобным и широко используе.мым является определение устойчивости, сформулированное А. А. Ляпуновым.

Для установления, устойчиво ли состояние равновесия необходимо к системе приложить некоторое возмущение (отклонить систему от состояния равновесия) н рассмотреть движение системы после снятия возмущения (т. е. собственное движение системы). Для линейных систем достаточно следующее определение устойчивости.

Устойчивая линейная система - после прекращения действия возмущающих сил система стремится к исходному состоянию, т. е. начальные отклонения стремятся к нулю.

Неустойчивая линейная система в собственном движении удаляется от состояния равновесия так, что отклонение непрерывно нарастает со временем.

Реальная неустойчивая система, удаляясь от состояния равновесия, со временем переходит в нелинейный режим. Чаще всего в этих случаях возникают автоколебания.

Для нелинейных систем необходимо оговорить, помимо того, степень начальных отклонений, поскольку система может иметь несколько состояний равновесия, из которых одни являются устойчивыми, а другие - нет.

Ниже рассматриваются только линейные системы.

Прямой путь определения устойчивости системы состоит в составлении уравнения, описывающего собственные-движения системы, и исследовании решения этого уравнения.

Дифференциальное уравнение составляется на основе знания передаточной функции замкнутой системы:

ф(Д)= евь,х(0 M(D)

ввх (О

N{D)

где М(Р) и N{D) - полиномы относительно D:

N(D) = щD + + ... + a

(причем для реальных систем- т < п).

Дифференциальное уравнение, описывающее свободные колебания в системе, имеет вид:

N(D) еБых = 0.

или

(floD + CjD - + . . . + й„) ввых = 0.

Движение системы будет затухающим, а система устойчивой, если действительные части корней характеристического уравнения

йо + + . . . + й„ = О

(цолученного заменой в N(D) = О оператора D на параметр Ъ) будут отрицательные. Если хотя бы один корень имеет положительную действительную часть, система будет неустойчивой.

На практике для определения устойчивости линейной системы пользуются критериями устойчивости, т. е. правилами, с помощьютсоторых можно определить устойчива ли система, не прибегая к решению дифференциальных уравнений.

Критерии устойчивости

Алгебраический критерий (Рауса^Гурвица) Для определения устойчивости составляется передаточная функция замкнутой системы Ф = .

Система автоматического регулирования будет устойчивой, если все коэффициенты а^, %.....я знаменателя

передаточной функции замкнутой системы

N(D) = aD + CiD - + . . . + й„

положительны (необходимое условие) и, кроме того, выполняются следующие неравенства:-

CjCa - > О для системы 3-го порядка (п - 3);

щаа^ - 4 - ОрО^ > О для системы 4-го порядка (п = 4);

+ Zaja-fifi - а^я > О для системы 5-го порядка (п = 5).

Невыполнение указанных неравенств свидетельствует о неустойчивости- системы.

При выполнении необходимого условия (коэффициенты положительны и отличны от нуля) системы, описываемые уравнениями 1 и 2-го порядков являются устойчивыми.

Пример 1. Автоматический пааенгатор прн наличии фильтра с постоянной времени Т (стр. 440).

Передаточные функции разомкнутой и замкнутой систем будут соответственно:

W(D) =

6 ТГ в05 + (Г + Гдв)02 [ £)

(20-15)

Ф(0) = =

Ввх .TTbD + (Tb + T)IP + D+Kv

следовательно,

N(D) = ГдзГО^ + (Тдв +T)D+D+ Кы

(20-16)

здесь

Со = ТрТ; щ = Гдв +Т: й2 = 1; Яз = Kv

Условия устойчивости:

fliCa - йдаз > 0; Гдв + Г - ГГдвЯ > О

или

= /С,

ДВ

(20-17)

Если Kv не удовлетворяет последнему неравенстйу (т. е. Kv > Ккр), система становится неустойчивой. В данном случае будут наблюдаться колебания антенны. Амплитуда их нарастает до некоторой величины, после чего в системе установятся автоколебания.

Пример 2. Система АПЧ с двигателем при наличии фильтра с постоянной времени Г (стр. 460).

Система описывается теми же передаточными функциями (20-15) и (20-16). Условие .устойчивости поэтому остается прежним (20-17). При его нарушении (т. е. когда К. > К^р) система становится неустойчивой. Однако проявляется эта устойчивость несколько иначе, чем в примере1: система выбивается из режима подстройки, и подстраивающее действие ее резко ослабляется.

Частотный (амплитудно-фазовый) критерий (Найквиста - Михайлова) Критерий позволяет установить устойчивость замкнутой, системы регулирования по aмплнтyднo-фaзoJ Ёым или логарифмическим характеристикам разомкнутой системы. Приводимые ниже определения относятся к системам, устойчивым в разомкнутом состоянии.

Определение устойчивости по амплитудно-фазовым характеристикам

Если точка с координатами (-1, /0) не охватывается контуром, образованным амплитудно-фазовой характеристикой и положительной вещественной полуосью, замкну- (гая система устойчива; если точка (-1,/ 0) расположена внутри него - система неустойчива (рис. 20-35) *.

Амплитудно-фазовые характеристики систем, для которых передаточная функция имеет вид инерционного звена или звена 2-го порядка, ни при каком К > О не охватывают точки -1, /О, поэтому они при К >О - устойчивы.

Определение устойчивости по лах и лфх

Замкнутая система устойчива, если на частоте, для которой ф= -п ордината лах разомкнутой системы имеет отрицательную величину. Если разомкнутая система устойчива, а лфх пересекает лннню -п в нескольких точках, система .будет устойчивой, когда L(to) < О при ф = -п для самой правой нз точек пересечения.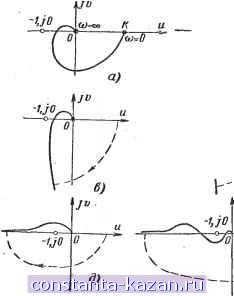

Рис. 20-35. Использование амплитудно-фазовых характеристик для определения устойчивости следящих систем.

а - устойчивая система с передаточной функцией разомкнутой системы вида

W = - . -

(7-,£> + I) {TD + 1) (TsD + D

б - неустойчивая система с передаточной функцией того же вида; в - устойчивая система с передаточной функцией разомкнутой системы вида

-

D{TD+l){TD+l)

г - неустойчивая систьма с передаточной функцией того же вида; Ь - неустойчивая система с передаточной функцией имеющей в знаменателе множитель е - устойчивая система того же вида.

В случае, когда система содержит интегрирующие звенья и амплитудно-фазовая характеристика при со О уходит в оо, для образования замкнутого контура необходимо провести дугу окружности бесконечно большого радиуса от действительной положительной полуоси до бесконечно удаленной ветви характеристики по часовой стрелке (рис. 20-35, е, ё).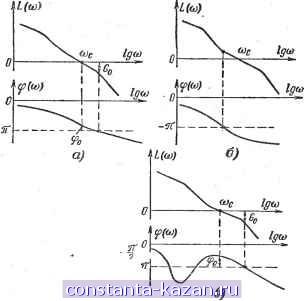

При нахождении точки - 1, /О на характеристике систему целесообразно считать неустойчивой, поскольку малейшее увеличение коэффициента усиления системы приводит к тому, что эта точка будет охватываться контуром.

Рнс. 20-36. Использование ЛАХ и ЛФХ для определения устойчивости.

а - система устойчива {Go и Фо - запас устойчивости по амплитуде и фазе); б - система неустойчива; в - система устойчива.

Частотный критерий широко используется в практике благодаря тому, что построение лах и лфх разомкнутых систем обычно не вызывает затруднений. В практике пользуются понятиями запаса устойчивости, характеризующими, насколько далека амплитудно-фазовая характеристика от критической точки (-1, /0).

Запас устойчивости по амплитуде Gq - количество децибел, на которое нужно увеличивать усиление на частоте, соответствующей фазовому сдвигу ф = -я, чтобы система потеряла устойчивость. На лах Gq отображается отрезком между осью абсцисс и ординатой лах для частоты, соответствующей фазовому сдвигу -п.

Запас устойчивости по фазе - угол фо = 180° - - ф(сй(.), где сй(, частота среза, т. е. частота, при которой лах пересекает ось абсцисс (модуль амплитудно-фазовой характеристики равен 1). На лфх фо есть угол превышения фазовой характеристики над линией ф = -п при частоте среза С0(,- При хорошем качестве процесса регулирования обычно выполняются условия Go > 10 дб; Фо > 30-45°.

Величины Фо и Go используются также для оценки качества регулирования.

2. Влияние корректирующих звеньев на устойчивость

Для придания систи,!е устойчивости и необходимых динамических качеств (см. ниже) вводятся корректирующие цепи: последовательные и параллельные.

В результате введения этих цепей амплитудно-фазовая характеристика деформируется так, что система из неустойчивой превращается в устойчивую.

Последовательные корректирующие цепи

В качестве последовательных корректирующих цепей обычно используются форсирующие нли интегродифферен-цирующие звенья. Действие форсирующего звена иллюстрируется примером.

Пример. Автоматический радиопеленгатор с учетом инерционности фазового детектора (стр. 440).

Критический коэффициент усиления до введения корректирующей цепи (стр. 441, формула 20-17):

Если ввести форсирующее звено UJk = T(fi + 1, передаточные функции разомкнутой и замкнутой системы будут соответственно:

ГдвТОз + (Где + Г) + D

{ТфР + 1)

ГдеГО + (Где +T)D + D + КТфй + Кг,

Следовательно, N(D) = TTD + (Где + T)D + (1 + + КуТф)0 + Kv. используя алгебраический критерий для системы 3-го порядка (стр. 441), найдем:

<J + --K.

1 + КиТф Тр

Этому неравенству можно удовлетворить при любом коэффициенте усиления Kv. выбирая Гф достаточно большим.

Соответствующие амплитудно-фазовые характеристики изображены на рис. 20-37, а.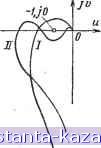

Рис. 20-37, Иллюстрация влияния корректирующих звеньев иа вид амплитудно-фазовых характеристик.

а - видоизменение амплитудио-фазовой характеристики прн введении последовательной коррекции (идеального форсирую-

щего звена); V5 =

0(7-двО-Ы)(?-С-Ц)

- передаточная характе-

ристика без коррекции; W =

.(ГфР + )

--с коррекцией;

-D(TD-\- ixro-fl) 6 - то же при параллельной коррекции; / - амплитудно-фазовые характеристики цепи без коррекции; II - с коррекцией.

Неудобство такой последовательной коррекции состоит в том, что

- необходимость приближения реального форсирующего звена, к идеальному вынуждает выбирать отноше-

ние Кф - (см. стр. 431) очень малым. Это приводит

к резкой потере усиления в последовательном контуре и, следовательно, к необходимости дополнительных усилителей, доводящих общин коэффициент передачи до требуемого значения;

- при ди(}х5)еренцировании сильно возрастает уровень помех в системе.,

Параллельные корректирующие цепи

В качестве таких цепей используются дифференцирующие, форсирующие или пропорциональные звенья, включаемые в цепь отрицательной обратной связи, охватывающей наиболее инерционные элементы системы. Пример охвата инерционного звена обратной связью см. на стр. 433. О влиянии корректирующих цепей на качество регулирования - см. также на стр. 452.

20-4. КАЧЕСТВО ПРОЦЕССА РЕГУЛИРОВАНИЯ 1. ОБЩИЕ СВЕДЕНИЯ

В практике возникает необходимость оценки качества автоматических систем, т. е. степени их пригодности для эксплуатации. О качестве системы судят по следующим показателям:

- точности работы в установившихся режимах при постоянных или медленно меняющихся воздействиях;

- виду и особенностям переходных характеристик;

- точности работы при случайных возмущениях. Выбор таких показателей качества обусловлен тем,

что они:

а) позволяют оценить точность системы для воздействий, часто всгречающихся в практике;

б) позволяют сформулировать удобные количественные требования к качес'тву процесса регулирования;

в) для многих автоматических систем эти показатели поддаются определению теоретически и экспериментально.

Характеристикой качества в установившемся режиме является ошибка 6 = 6ех - ввых. которая имеет место в системе после окончания переходных процессов (т. е.-после того, как собственные движения системы затухли).

Характеристиками качества системы являются также (рис. 20-38):

- вид переходной характеристики (монотонная, без выбросов, с выбросами и т. д.);

- время регулирования tp от момента подачи сигнала включения до момента, начиная с которого отличие переходной характеристики от ее установившегося значения не превосходит заранее обусловленной величины (обычно 5%);

- количество и величина отдельных выбросов (пере- ь регулирований): Aj, Да.....

Характеристикой качества при действии случайных возмущений является ошибка воспроизведения, т. е. разница между полезным входным сигналом бвх.с (т. е. тем сигналом, который должна воспроизвести система) и выходным сигналом, который имеется в действительности.

Так, если на вход системы действуют полезный сигнал бвх.с и мешающий сигнал (помеха) бвх.п. то ошибка воспроизведения

о.в - вх.с - вых-Так как бвых = (бвх.с + бвх.п).