где Ф{0)

1 + W

- передаточная функция системы, то

вх-с

Оо.в-jqr-jqrr вх.п =

= Фе(0)еЕх.с-Ф(0)евх.п(*).

Первая составляющая ошибки воспроизЬедения представляет динамическую ошибку системы, вторая - ошибку, вызванную действием помехи. Сигнал и помеха являются случайными функщ1ями времени. Поэтому ошибка воспроизведения является также случайной функцией

Рнс. 20-38. Различные виды переходных характеристик Я (0-

а - немонотонная без перерегулирований; б - монотонная; в - с перерегулированиями и А ; -время регулирования; А (?) - отклонение выходной величины от установившегося значения (динамическая ошибка); д„ - стслонение от установившегося значения, при котором производится стечет t (обычно ±5%).

и ее выражают через одну из характеристик случайных функций. Для наиболее важных в практике случаев действия стационарных входных сигналов удобной характеристикой является среднеквадратичное значение.

С расширением полосы пропускания системы динамическая ошибка (первое слагаемое (*)) уменьшается, однако, увеличивается ошибка, вызванная действием помех (второе слагаемое бо.в)-

Здесь имеют место аналогичные явления, что и в приемном устройстве при изменении полосы пропускания: с расширением полосы увеличивается точность воспроизведения входного сигнала, но одновременно растет уровень шума, обусловленный действием различного рода помех.

Одна из задач синтеза систем регулирования состоит в выборе структуры и параметров, при которых обеспечивается минимально возможное значение ошибки воспроизведения (чаще всего среднеквадратического значения ошибки бо.в)-

2. УСТАНОВИВШИЕСЯ РЕЖИМЫ

После затухания переходных процессов система переходит в установпвшийся режим. Показателем качества в этом режиме является точность системы при постоянных

и меняющихся по определенному закону воздействиях (чаще всего вида бвх = afi, где с - постоянная, а fe = 1, 2, 3).

Постоянные воздействия (или возмущения)

Установившаяся ошибка \ при постоянном воздействии (возмущении) находится с помощью соответствующей передаточной характеристики, в которой следует положить D ~ Q.

Постоянное входное воздействие-Ь^хя

Согласно общему ввфажению для ошибки [формула (20-И), стр. 437]

ео = Фе(£)евхо

1 -f W (0)

в статической системе W (Q) = К - коэффициент передачи разомкнутой системы. Поэтому в такой бистеме устанавливается ошибка (рнс. 20-39, а)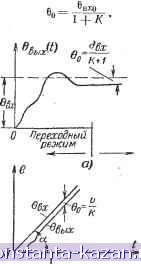

Nc/панобиВ-шийся режим

f-- .

Переходный !станоВи6шийсР аежим режип^

Рис. 20-39. Переходный процесс и установившаяся ошибка в статической н астатической системах при различных входных воздействиях.

а - р,ля статической системы при постоянном входном воздействии; установившаяся ошибка б^; б - для системы с астатиз-мом 1-го порядка при линейном нарастании-входного сигнала; установившаяся ошибка е„.

Относительная ошибка s = = ыхо

БХО бвхО

= I К называется статизмом системы. Чем выше К,

тем меньше ошибка, тем точнее система.

В астатической системе (стр. 437) в установившемся режиме

M(D)

= Фф)

0=0 D*/?j(D) + M(D) D=D

= 1.

Следовательно, Вех = бвхо и бц = 0. Астатическая система в установившемся режиме при постоянном входном воздействии ие дает ошибки.

Постоянное воздействие на регулируемый объект

улируем! шие [фор

При воздействии на регулируемый объект возмущения П возникает рассогласование [формула (20-14),стр. 438]

Ht) =

l+F(D)B(D)

W = -

Следовательно,

DRi (D)

М

6(0 =

м

М

При D О (в установившемся режиме)

Do - - щ.

Воздействие, приложенное ко входу, вызывает равное но противоположное по знаку рассогласование.

Пример 1. Система АПЧ с однозвенньм или двухзвенным фильтром (стр. 439). Для такой системы

К

(D) =

TD + 1 /С

и W (D) =

В установившемся режиме при постоянном воздействии Пд ошибка

l+f(0)B(0)-

Наиболее интересен в практике случай, когда ш F отличаются только множителем (стр. 438): Fa{D) = KtiF(D) (воздействие приложено ко входу объекта). Для этого случая

nj( F(0) l+f(0)B(D)-

Ошибка равна нулю только в том случае, если звенья В (D), предшествующие объекту, содержат хотя бы одно интегрирующее звено. Действительно, при этом

B(D)=;

DRiD)

Me (0) 0; Rb (0) 0; В (0) = со и во = 0.

Постоянное воздействие на входе системы Sni В этом случае (стр. 437)

в установившемся режиме:

для статической системы

При достаточно большом я Во = - вп1, и система имеет ошибку, практически равную внешнему воздействию; для астатической системы

M{D)

TJ-J + (71 + 72 + Гс) О + 1

Система является статической, так как не содержит интегрирующих звеньев.

При отклонении частоты сигнала на величину А/;, промежуточная частота отклоняется от номинального

значения на величину Д/о= , ] Jk -J-Д^. Вели-

1 + А Лп

чина /Сп = I + К = 1 + КрКу называется коэффициентом автоподстройки (обычно 10-50).

При изменении температурных условий частота гетеродина отклоняется на Д/г.п.(стр. 438). Поэтому изменится промежуточная частота (возникнет рассогласование)

Мг.п \ + W{P)

1 +/С

A/r.n

причем А/о < Д/r (A Г - изменение температуры, Kt - уход частоты гетеродина при изменении t иа 1°С).

В результате внешних воздействий изменяется переходная частота дискриминатора на Д/д. Это эквивалентно добавлению ко входу системы той же величины Д/д. В результате в замкнутой системе изменится промежуточная частота на величину (возникнет рассогласование)

Д?о=--г^д/ -д/д.

Таким образом, при нестабильности переходной частоты дискриминатора возникают отклонения промежуточной частоты, примерно равные Д/д и значительно большие, чем при нестабильности гетеродина.

Пример. 2. Автоматический радиопеленгатор (стр. 440) - система астатическая, так как содержит одно интегрирующее звено:

а) при изменении выз^одного угла Вех остаточная ошибка в установившемся режиме равна нулю;

б) при действии ветра 77е на антенну возникает ошибка (стр. 439).

ПвКпКцв

0(ГдвО+1)+/С„

Ошибка пропорциональна силе ветра и обратно пропорциональна коэффициенту усиления по скорости. Заметим, что эта ошибка не зависит от числа и постоянных времени инерционных звеньев, предшествующих двигателю.

Воздействие, изменяющееся по линейному закону

Постоянной отличной от нуля ошибкой при таком воздействии характеризуется система с астатизмом 1-го порядка, для которой передаточная функция разомкнутой системы имеет вид:

Ф>- DRiD) - e{t)

Если Вех изменяется по линейному закону с постоянной скоростью libx, то для указанной системы в установившемся режиме выходная величина изменяется с той же скоростью

и в системе имеется постоянное рассогласование, т. е. ошибка (см. рис. 20-39, б).

00=--> At)

- коэффициент передачи системы (называемый также добротностью или коэффициентом усиления по скорости). Величина Kv равна произведению коэффициентов передачи всех звеньев, т. е. коэффициенту передачи разомкнутой системы. По величине Kv можно судить о том, какова йудет скорость изменения выходного сигнала, если на вход, разомкнутой системы подать единичный сигнал. Например, если следящая система имеет Kv = 50 1/сек, то при рассогласовании в 1° скорость вращения двигателя при

зазомкнутой цепи обратной связи будет равна 50°/сек.

Рассогласование во называют иногда скоростной ошибкой системы.

Пример. Автоматический радиопеленгатор (стр. 440). Передаточная функция разомкнутой системы

W{D) =

0(ГдвО + 1)

M{D) = Kv - коэффициент передачи системы;

Следовательно, ОбвыхСдвС + 1) = Kvd-

Но Обвых = бвых = г'вых - скорость изменения

выходного угла (поворота антенны пеленгатора). Следовательно, v(TpjP + 1) = /Сов.

Для установившегося режима D = 0; v= VeboC.

Так как между входной и выходной величинами имеется постоянная ошибка Во, то и входная величина изменяется с той же скоростью (рис. 20-39), т. е. tBx = вых. так что

Тот же результат можно получить проще, записав выражение для

) = вх

l + W D{l-\-W) DW M(D)R(D)

(скорость изменения постоянной величины - единицы равна нулю, т. е. D1 = =0J.

В установившемся режиме D = О и Во ==

Полученный результат имеет простой физический смысл. Пусть пеленгатор следит за радиостанцией, установленной на самолете, летящем по окружности с центром в точке установки пеленгатора. Тогда последний будет указывать положение самолета с постоянной ошибкой бц. Именно благодаря этой ошибке на якоре двигателя будет иметь место напряжение, приводящее в движение антенну, в результате чего последняя следит за самолетом. Чем больше коэффициент передачи системы Kv, тем при меньшем угле рассогласования бц будет достигнуто напряжение, необходимое для обеспечения данной скорости вращения якоря двигателя. Чем выше угловая скорость движения tBx самолета, тем при данном Kv больше скорость вращения

якоря двигателя, тем, следовательно, должна быть больше ошибка вц.

Система с астатизмом 2-го порядка не имеет скоростной ошибки. Установившаяся ошибка возникает, если входная величина изменяется с ускорением. При квадратичном законе (равноускоренное движение) эта ошибка будет постоянной.

3. Переходные (неустановившиеся) режимы

Неустановившиеся режимы принято оценивать по виду переходной характеристики Я(/). Для систем, описываемых передаточными функциями звеньев инерционного и 2-го порядков, пользуются стандартными графиками (рис. 20-14, ж и 20-16 3),

Пример. Построение переходной характеристики для системы АПЧ с двухзвенным фильтром.

Замкнутая система описывается передаточной функцией

Ф(0) =

хЮ -f 2gTD + 1

где Ks, т и g выражаются через параметры системы (см. стр. 440). По известной величине выбирается кривая из стандартного графика на рнс. 20-16, з, которая затем перестраивается в необходимом масштабе.

Для более сложных систем переходный процесс определяется приближенными методами, в частности методом трапецеидальных характеристик . Последний основан на интегральном соотношении, связывающем переходную характеристику H{f) с вещественной частотной характеристикой Р{ч>) замкнутой системы

H{t) =

Р (со) sin a)t Ф

(20-18)

На основе связи H{t) и Р(сй), выражаемой равенством (20-18), можно сформулировать следующие положения:

1. При изменении величины Р(со) в некоторое количество раз H{t) изменяется во столько же раз.

2. При увеличении (уменьшении) масштаба частот /характеристики Р(ч>) в некоторое количество раз, во столько же раз уменьшается (увеличивается) масштаб времени переходной характеристики H{t). Отсюда следует: чем шире полоса частот, в пределах которой Р(со) имеет еще существенную величину, тем быстрее протекают переходные процессы.

3. Переходная характеристика для Р(сй) может быть получена путем разбиения Р(сй) на отдельные слагаемые Pj(cu), Р2(со), и т. д. и суммирования переходных характеристик, найденных для каждого из этих слагаемых.

4. Участок действительной частотной характеристики

для частот, начиная с которых < 0,1, можно.отбро-

сить (т.. е. считать для этих частот Р(Ч)) = 0).

5. Близким действительным частотным характеристи-. кам соответствуют близкие переходные характеристики.

Это свойство может быть облечено в более строгую мате-. матическую форму, устанавливающую количественные соотношения между приближениями для частотных и временных характеристик.

6. Величина Р (0) равна пределу, к которому стремится переходная характеристика при t со. Это гово-

,1

Предложен В. В. Солодовыиковым.