рит о том, что для астатической системы Р (0) = 1; для

статической Р (0) = -.

1 + д

Свойства 3, 4 и 5 позволяют заменить частотную характеристику Р (сй) близкой по форме, но более простой, например состоящей из прямолинейных отрезков, и разбить затем полученную фигуру на более простые.

Рис. 20-40. Стандартная характеристика Р (ш), для которой составлены таблицы Л-функций 1Л (t)].

При использовании метода трапецеидальных характеристик исходную кривую Р (со) заменяют отдельными трапециями так, чтобы в сумме получалась фигура, близкая к исходной.

Для частотной характеристики Р (ш), имеющей вид

трапеции с определенньм наклоном стороны к =

и соо = 1 (рис. 20-40) при Р (0) = 1, составлены таблицы стандартных переходных функций (Л-функцнн), соответствующих элементарным трапециям с различными параметрами У. (табл. 20-1). Таблица построена в зависимости

от т - соц^ путем вычисления интеграла (20-18). Для каждой из полученных при разбивке Р (со) трапеций необходимо сделать пересчет масштабов:

- по оси ординат в Р (со) раз;

- по оси времени растянуть (при сОц > 1) или сжать прн < 1) во столько раз, какова величина сОц,

Действительное время t и табличное время % й-функ-

ций связаны соотношением t = ~

Проделав указанную операцию для каждой из трапеций и суммируя полученные кривые, находим результирующую переходную характеристику, соответствующую исходной, частотной характеристике Р (со). Вещественная частотная характеристика Р (со) замкнутой системы находится по логарифмическим амплитудной и фазовой характеристикам разомкнутой системы путем использования номограммы (рис. 20-42). Методика построения Н (t) рассматривается на примере.

Пример. Автоматический пеленгатор при наличии фильтра (стр. 440).

Передаточная характеристика разомкнутой системы

W (D) = =

е о(ГдвО + 1)(го + 1)-

Примем Кг, = 15 1/сек; Гд = 0,02 сек; Т = RC = 0,01 сек - постоянная времени фильтра.

Построение переходной характеристики состоит из следующих этапов:

1. Построение ЛАХ и ЛФХ разомкнутой системы по заданной W (D) (рис. 20-41).

ЛАХ. На частоте со - 1 откладывается величина 20 lg/(o = 20 lg 15 = 23,4 дб (или на оси частот величина

Таблица й-функций

Таблица 20-1

О

9 10 II 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

0,000 0,138 0,310 0,572 0,755 0,857 0,896 0,903 0,904 0,910 0,924 0,939 0,947 0,950 0,950 0,952 0,956 0,961 0,965 0,966 0,967 0,967 0,968 0,971 0,974 0,975 0,975 0,975

0,000 0,176 0,340 0,628 0,828 0,938 0,978 0,982 0,979 0,985 0,997 1,009 1,015 1,015 1,012 1,011 1,012 1,015 1,016 1,015 1,015 1,013 1,011 1,011 1,011 1,010 1,008 1,007

0,000 0,192 0,371 0,683 0,896 1,008 1,042 1,037 1,024 1,020 1,025 1,031 1,031 1,024 1,015 1,009 1,007 1,006 1,005 1,002 0,998 0,995 0,994 0,995 0,996 0,996 0,995 0,995

0,000 0,207 0,401 0,732 0,958 1,060 1,087 1,065 1,037 1,021 1,018 1,019 1,014 1,004 0,994 0,988 0,988 0,991 0,991 0,995 0,995 0,995 0,997 1,000 1,004 1,005 1,005 1,004

0,000 0,223 0,432 0,786 1,013 1,110 1,112 1,068 1,023 0,998 0,992 0,993 0,993 0,988 0,985 0,985 0,991 0,998 1,005 1,008 1,006 1,005 1,004 1,004 1,003 1,002 1,000 0,997

0,000 0,240 0,461 0,833 1,061 1,142 1,118 1,051 0,993 0,966 0,970 0,982 0,993 0,997 0,997 1,000 1,005 1,011 1,012 1,008 1,001 0,996 0,995 0,996 0,998 1,000 1,000 1,000

Kv= 15 Усек) и через полученную точку проводится прямая с наклоном - 20 дб/дек (это соответствует интегри-Kv

. рующему звену -).

После 1-й частоты сопряжения

= 50 Усек, вследствие наличия инерционного звена

наклон ЛАХ увеличивается еще на -20 дб/дек и будет составлять - 40 дб на декаду. После 2-й частоты сопря-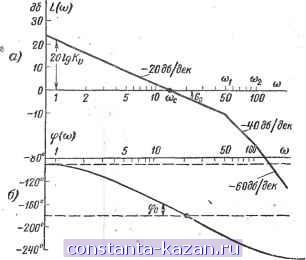

Рис. 20-41. ЛАХ и ЛФХ разомкнутой системы с передаточной функцией.

W (О) =

D (7- D-H) (TD + 1) D (0,02С -Ь 1-) (O.OID -Ц)

ш, = - = 50 1/сек; = -L-= ЮО 1/сек - частоты сопряже- дв

НИИ; Ор -запас устойчивости пр амплитуде (5 дб); фд - запас устойчивости по фазе (18°); ш^, - частота среза (12 1/еек).

жеиия-г = 100 Усек наклон ЛАХ вследствие наличия

2-го инерционного звена увеличивается до - 60 дб на декаду.

ЛФХ. Фазовая характеристика строится путем доба-

вления к прямой -~- (фазовый сдвиг интегрирующего

звена) фазовых характеристик двух инерционных звеньев.

Суммарная ЛФХ при со -> со стремится к прямой-- п.

2. Построение Р{а>). Для выбранной частоты Ф по известным ЛАХ и ЛФХ L (со) и ф (со) с помощью номограммы рнс. 20-42 находится точка Р (со). Так, для частоты ю -= 5 1/сек L (5) = + 8 дб; ф (5) = - 125°. На номограмме этим данным соответствует точка А (5), лежащая на кривой Р с индексом 1,1 (т. е. Р (5) = 1,1). Для со = = 40 Усек L (40) = - 10 дб; ф (40) = - 204°; точка А (40) лелснт вблизи-кривой с индексом -0,4, т. е. Р (40) = -0,35 и т. д. Так, по точкам построена кривая Р (ш) (рис. 20-43,а).

3. Разбиение Р{(л) на трапеции (рис. 20-43,6) производится каждый .раз в соответствии с видом кривой Р (со). В данном случае Р (со) можно изобразить четырьмя отрезками прямых. Полученная фигура является суммой трапеций / + 4- / -ф- IV. Характерные частоты ю/== = 10 Усек; со = 20 Усек; Ojjj = 40 Усек; (И/у = 100 Усек.

В результате сложения всех трапеций образуется фигура, близкая к исходной действительной частотной

характеристике Р (со) (иа рис. 20-43, а показана пунктиром).

4. Нахождение переходной характеристики H{t) (рис. 20-43, в, г).

Строятся переходные характеристики для каждой из трапеций: hj (т); ft (т); ft / (т); hjy (т).

Трапеция I.

. = -10 0,5. СО 20

По таблице ft-функций находим колонку к = 0,5 и выписываем зависимость ft/ (т). Затем изменяем масштабы: по оси ординат - растягиваем в Р/(0) = 2,64 раза и по оси времени -слснмаем в сй = 20 раз. В результате находим Я/ (/). При / оо. Я/ (f) -> 2,64.

Трапеция II. nji = - = 0 (первая колонка ft-функ-со/

ций). Величины ft этой колонки увеличиваем в Р (0) = = - 0,44 раза; по оси времени сжимаем масштаб в Ю/ = = 10 раз. В результате получаем Я (i). Трапеция III.

ш 20

и^/ --= -= 0,5.

СО / 40

По оси ординат данные h (т) для колонки и = 0,5 умножаем на -0,8; по оси абсцисс данные т делим на сй / = = 40. Находим Я /(/). Трапеция IV.

to / 40

Я/1/ =- = - 0,4.

CO/V 100

По оси ординат данные для ft (т) умножаем на -0,4; по оси абсцисс данные времени т делим на 100. Находим Hiv И).

Для получения переходной характеристики Н {t) суммируем полученные кривые:

Я (t) = Я/ (t) + Hjj (t) + Я / (О Ф Hiv (t).

В данной системе имеет место значита1ьное перерегулирование (около 70%) и сравнительно большое время регулирования tp = 0,5 сек (отсчитывается на уровне, отли. чающемся на ±5% от установившегося).

При > оо характеристика Я (f) стремится к Р(0) = 1. Этого следовало ожидать, поскольку система является астатической.

4. Влияние корректирующих устройств на качество процесса регулирования. Элементы синтеза линейных систем

Связь качества регулирования с характеристиками разомкнутых систем

Если качество процесса регулирования для заданных параметров не удовлетворяет поставленным требованиям (например, велико tp, Aj, Ag и т. д.), то в систему вводят дополнительные корректирующие элементы и выбирают их характеристики так, чтобы удовлетворить этим требованиям.

Подбор параметров корректирующих элементов проводится путем использования ЛАХ и ЛФХ разомкнутой системы. Для наиболее часто встречающихся в практике, минимально фазовых систем i достаточно использовать

Минимально-фазовыми называются системы, для кото-, рых действительные значения корней уравнений М (D) = О и R (Р) = О [лг (D) - числитель и R (D) - знаменатель передаточной функции разомкнутой сястемы] неположительны. К этому типу относятся все рассмотренные ранее динамические звенья. Примером неминимально фазовой системы является, например, мостиковая цепь с i? и С элементами.

Рис. 20-42. Номограмма для пересчета ЛАХ и ЛФХ разомкнутой системы в действительную частотную характеристику Р{а) замкнутой системы [точки А (5) и А (40) соответствуют частотам (0 = 5 1/сек и й) = 40 1/сек].

-320 -зво -гво-гво-г'/в-гго -zoo -wo -wo -шо -izo-wo -во -ео -w

¥\

Рнс. 20-43. Построение переходной характеристики системы.

с - действительная частотная характеристика, построенная согласно номограмме (пунктиром обозначена приближенная характеристика); б - разбиение действительной частотной характернстики Р (ш) на трапецеидальные I - IV (пунктирная фигура - приближенная характеристика); в - ft-функции для трапеций Лу - Л/\/; S - построение суммарной (переходной) характеристики Н (t)= Hj (/)-f-+ О) + H j {t) + Hjy U) (характеристики fi-li I- Н11 j, H1У построены путем пересчета масштабов характеристик h, - h.y).