только ЛАХ разомкнутой системы, поскольку ЛАХ и ЛФХ в таких системах связаны определенной зависимостью.

При подборе корректирующих цепей сначала строится желаемая ЛАХ.(т. е. такая ЛАХ, для которой переходная характеристика имеет благоприятную форму и заданное tp). Затем путем вычитания жаааемой JIAX из действительной находят ЛАХ корректирующей цепи, по которой затем определяют вид и параметры этой цепи. Решающее влияние на характер переходного процесса имеет вид ЛАХ на средних частотах вблизи частоты среза о^-

Установлено, что благоприятное протекание переходного процесса имеет место только в том случае, если ЛАХ вблизи сй(, имеет наклон -20 дб на декаду, причем длина этого участка должна быть порядка одной декады.

Низкочастотный участок ЛАХ определяет поведение системы в установившемся режиме. В астатической системе наклон ЛАХ на этих участках -20 k (k - порядок астатизма); в статической k = О и наклон О дб на декаду.

Высокочастотный участок (при со сос) существенного влияния на переходную характеристику не оказывает; сн определяет характер прохождения высокочастотных составляющих.

годё/ден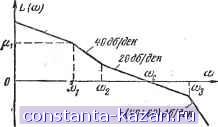

Рис. 20 44 Типовая ЛАХ автоматической системы, для которой построены номограммы.

Для подбора желаемой ЛАХ имеются номограммы, справедливые для ЛАХ типа изображенной на рис. 20-44. Однако этн номограммы (рис. 20-45) дают также приемлемые результаты для статических систем и астатических систем с наклоном ЛАХ на участке tOj-со 2 -60 дб на декаду. Номограммы (рис. 20-45) позволяют определить следующие данные (рис. 20-46):

- время регулирования (отсчет на уровне 0,95 от установившегося значения); ty - время достижения первого выброса; Нт - максимальное значение первого выброса; (П' - величину максимума амплитудно-частотной характеристики замкнутой системы и частоту, на которой он достигается.

На номограммах некоторые показатели отнесены к частоте Юр. Подбор желаемой ЛАХ требует определенных навыков.

Для грубых прикидок используются следующие

соотношения: /т,-; желательное отношение частот

2 < - < 4; протяженность участка вблизи Юс должна

СОс

быть возможно большей и иметь порядок одной декады. Путем нескольких проб с учетом приведенных соотношений выбирается желаемая ЛАХ и находятся параметры корректирующего звена.

Пример. Дана шстема с передаточной функцией (рис. 20-47)

W (D) =

0(Гдз0 + 1)(Г0+ 1) Kv = 70 1/сек; Гд = 0,1 сек; Т = 0,02 сек.

Требуется подобрать корректирующую цепь, прн которой время регулирования = 0,3 сек, а < 1,3; <р < 2/у. При данных параметрах система неустойчива, так как

1 , 1

/<Kp=7 + -v= 10 + 50 = 60 </(о.

Выбираем

Юс = 4 р = 13,4 1/сек.

Соотношение ю/Юр < 4 определит ориентировочное значение < 4Шс. Выберем Шд = 4Шс = 53,5; Юг = 4 1/сек; Юд = 50 1/сек (длина участка - Юд несколько больше декады). Сопрягаем участок cog - Шд с низкочастотным участком прямой с наклоном -40 дб на декаду (целесообразно строить желаемую ЛАХ так, чтобы наклон соседних участков отличался на 20-40 дб/дек. Это облегчает подбор корректирующих цепей). Таким образом, определится Hj = 40 вб и = 0,8 1/сек. По номограмме (рис. 20-45), соответствующей отношению ш/Юс = 4 для

(J-i = 40 Эб и -i = 5ff = 0,061, находим: Юс 1о

- = 0,3; =0,42; ю„/Юс = 0.5,

г =1,18; Ф„=1.2.

= 0,5-13= 6,5 1,сек.

ty = -j= 0,21 сек; = 0,36 сек; ю^

Переходная характеристика удовлетворяет поставленным требованиям, и полученная ЛАХ может быть принята за желаемую. Разность между действитачьной и жаааемой ЛАХ дает ЛАХ корректирующей цепи: корр = L (и) - (w)- Иллюстрация построения этих ЛАХ для данного примера дана на рис. 20-47.

Корректирующие цепи

Используются: а) последовательные и б) параллельные корректирующие цепи.

Последовательные цепи

Наиболее употребительны: форсирующее звено (рис. 20-21), интегрирующий контур (рис. 20-48), интегро-диффеоенцирующий контур (рис. 20-49).

Пример, (продолжение предыдущего примера). Наиболее близкой к ЛАХ корректирующей цепи является ЛАХ интегроднфференцирующего контура.

Согласно рис. 20-47 и 20-49 имеем:

ч = -R А=4; == т =

Т2=/?С,=~=Гдв = 0,1 сек; Т^=. - =.-.

1,25 сек; Гг = - = 0,02 сек.

г/ г

1,6 ¥

I о,г о

0,01

1Ш

г,ч 2,г г

},S 1,2

0,0?

Для aij/WgV

¥

1,2 I

г,ч г,2

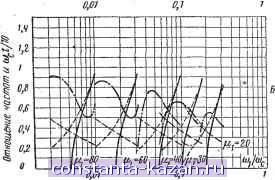
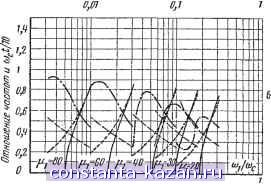0,01 0,1

или Wj/W=°°

Рис. 20-45. Номограммы для расчета желаемой логарифмической амплитудной характеристики. Номограммы построены для различных отношений а^/а^при условии, что наклон характеристики между (о^ и со составляег -40 дб на декаду, и для частот выше юз-бОбб/йек. - угловая частота колебаний на переходной характеристике.

- т------*т: = - >t/ c- m/V- -----Vy/10: - Vp/O-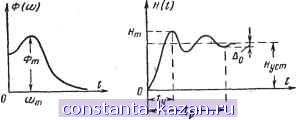

Рис. 20-46. Показатели качества системы 1Ф ((о) - амплитудно-частотная характеристика замкнутой системы, Н U) - переходная характеристика замкнутой системы].

Если имеющиеся в распоряжении корректирующие цепи имеют ЛАХ, только приближенно соответствующие Lkopp. после расчета целесообразно построить переходную характеристику, пользуясь методом трапецеидальных характеристик (см. стр. 448).

Параллельные цепа

Такт цепи включанзтся в линию отрицательной обратной связи, охватывающую наиболее инерционные звенья системы.

В качестве параллельных стабилизирующих цепей чаще всего используются:

дифференцирующее звено (см. рис. 20-20);

- дифференцирующие звенья, состоящие из двух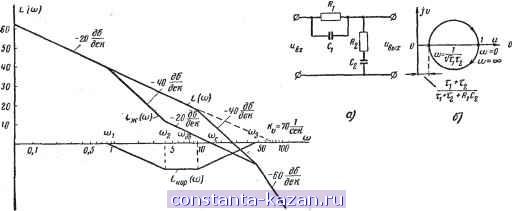

Рис. 20-49. Интегродифферейцирующий контур

Iff (С)

т =

(Т^Р -Ь 1) (TD -Ь U

2т,т2

Рис. 20-47. Построение ЛАХ корректирующей цепи. Исходная система описывается передаточной функцией

D{TD + l){TD + l)-

Цш) - ЛАХ исходной системы; J 1

D(0,lD + l)(0,02D-(-l)

((0) - желаемая LQppW - ЛАХ корректирующей цепи;

50 1/сек.

10 1/сек:

Ъ + RiCi Т + Н,Сг) - 4т.tj

Тг + Тг=-1,-+Г2 + К1Сг. схема; б - влшлитудно-фазовая характеристика; в - ЛАХ.

последовательно соединенных ячеек (двухзвенный RO фильтр верхних частот) с параметрами С^, Сц, Передаточная функция такого фильтра

L(w)

вых (t) вх(0

72£)2 2t,TD + 1

Рис. 20-48. Интегрирующий контур \У(С) =

Т^= RRCjfii i?iCi: 72= RCi,

T, + T+Rfi 2Vt,T,

вых

(контур выполняет операцию, лишь отдаленно напоминающую интегрирование), о- схема; б - амплитудно-фазовая характеристика; в - ЛАХ.

Из соотнощення Т^- = RjC+ Ri+ RyC находим

RiCi== 1,25 0,02 - 0,1 = 0,92 сек. Одним из параметров следует задаться, например емкостью Cj = 1 мкф. Тогда

?1 = = 0.92 Мол.; Cl== = 0,27 мкф;

0,92

i?.i=-V = 0,l Мом

При охвате звена звеном отрицательной обратной связи (рис. 20-50) расчет корректирующей цепи производится следующим образом. Следящая система приводится к простейщей, состоящей из звена с передаточной функцией W (D) (система без коррекции) и звена с передаточной функцией эквивалентного последовательного корректирующего звена W, как было описано ранее (стр. 435):

W(D)= W{p) W{D): .

WAD)

1 -f 1 + A