§ 22-7] Назначение и области применения электронных вычислительных машин

4) триггер - спусковая схема, имеющая два устойчивых состояния, сопоставляемых с двумя символами (О и I) двоичной системы счисления (рис. 22-5).

5) избирательная схема - многополюсник с т входами и п выходами, обеспечивающий вполне определенную комбинацию сигналов на выходе, соответствующую одной или нескольким вполне определенным комбинациям сигналов на входе (рис. 22-6).

Мод

с у м м ы

т

п-й разряд

3-й разряд

г-й разряд

t-u разряд

слагаемых

Рис. 22-8. Сумматор на триггерах. При поступлении кода первого-числа цепочка триггеров запоминает его. При поступлении кода второго числа происходит поразрядное сложение. Если в каком-либо разряде обоих слагаемых стоит единица, то соответствующий триггер устанавливается в положение нуль и образуется сигнал переноса, который через линию задержки (ЛЗ) передается в старшчй разряд (время задержки должно быть больше времени опрокидывания триггера).

На рис. 22-7 и 22-8 показаны комбинации основных элементов, обеспечивающие выполнение специальных задач.

когда процессы в модели имеют ииую физическую природу, но одинаковое с изучаемым явлением математическое описание.

В основе математического моделирования лежат законы подобия различных по своей природе физических явлений. Подобие проявляется, в частности, в том факте, что многие процессы, имеющие различную физическую сущность, описываются одинаковыми математическими уравнениями. Например, закон всемирного тяготения описывается уравнением

/2

показываюцщм, что сила взаимного притяжения F двух тел с массами и'гпг прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между телами.

Совершенно такую же форму имеет закон взаимодействия двух электрических зарядов, только вместо масс необходимо взять величины этих зарядов.

Наиболее удобной для изучения и воспроизведения в лабораторных условиях является область электрических явлений, поэтому наибольшее значение имеют методы электрического моделирования.

Моделирующей установкой называется устройство, структура которого может изменяться таким образом, чтобы происходящие в нем процессы описывались уравнениями, подлежащими исследованию.

22-6. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ НЕКОТОРЫХ ОТЕЧЕСТВЕННЫХ ЭЛЕКТРОННЫХ ЦИФРОВЫХ МАШИН

в последнее время используется память на ферритах емкостью I 024 числа.

22-7. НАЗНАЧЕНИЕ И ОБЛАСТИ ПРИМЕНЕНИЯ ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН НЕПРЕРЫВНОГО ДЕЙСТВИЯ

Механизация вычислительных работ может осуществляться не только путем численного реше.ния сложных математических задач на машине, но и путем моделирования (воспроизведения) явлений, подлежащих исследованию.

Моделирование может быть физическим, когда процессы в модели имеют ту же физическую природу, что и в исследуемом объекте, или математическим.

Величины, характеризуюцще изменение процессов в модели, изменяются непрерывно во времени. По этой причине моделирующие устройства называют также в ы-числительными машинами непрерывного действия.

На электронных моделях решение исследуемых уравнений получается в форме электрических напряжений, регистрируемых с помощью шлейфовых или электронных осциллографов.

Точность решения задач на электронных моделях составляет величину 1-5%, что вполне достаточно для целого ряда практических случаев.

Область применения электронных моделей очень сб-

ширна и охватывает следующие наиболее важные для техники вопросы:

1) исследование и проектирование систем автоматического регулирования и управления машинами и производственными процессами;

2) испытания реальной аппаратуры автоматического регулирования и управления;

3) анализ линейных и нелинейных электрических цепей и систем.

ров, а чаще - от того и другого. Так, например, температура, влажность и давление воздуха зависят от времени года и суток. Скорость самолета зависит от расхода горючего и высоты полета.

Если некоторая переменная величина у зависит от другой переменной величины л:, то говорят, что у есть функция X, и наличие такой зависимости записывают в виде выражения

у = f(x) или у= у (х).

щение

Уравнений обгекта (модель

Возмущение

Уравнения регулятора (модель)

Входной

Уравнения объеита (модель)

Переходное устройство

Реальный регулятор

Входной

Возмущение

Реальный объект

Уравнения регулятора (модель)

Входной

Рис. 22-9. Варианты использования электронных моделей для исследования систем автоматического регулирования.

а - моделирование всех звеньев системы для отыскания ее структуры и параметров, удовлетворяющих техническим условиям; б - проверка реального регулятора на модели объекта (переходные устройства - ЯУ предназначены для связи модели с регулятором и наоборот); в - подбор на модели структуры регулятора для реального объекта.

Способы построения решающих элементов электронных моделей используются при создании специализированных счетно-решающих устройств, применяемых в системах управления машинами и производственными процессами.

Важным свойством электронных моделей является простота их сочленения с реальными объектами для совместной работы (рис. 22-9). Это позволяет в лабораторных условиях проводить достаточно всесторонние исследования и испытания отдельных реальных узлов сложных систем. Это свойство моделей позволяет всесторонне исследовать поведение машины или системы машин в процессе проектирования, не конструируя их, что дает огромный экономический выигрыш. Модели, например,- позволяют в лаборатории исследовать наиболее сложные и опасные режимы полета нового самолета, не выполняя испытательного полета.

22-8. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ, ИЗМЕНЯЮЩИХСЯ ВО ВРЕМЕНИ

Переменные величины, функции и их производные

Многие параметры, характеризующие то или иное физическое явление или процесс, являются переменными величинами, зависящими от времени и от других парамет-

Под математической функцией следует понимать закон, связывающий взаимные изменения переменных величин.

В выражении у = f {х) переменная у является зависимой переменной или функцией, а переменная х является независимой переменной, так как ее значения выбираются в общем случае произвольным образом, и называется аргументом.

При решении технических задач требуется с помоцЦ)Ю математических формул и уравнений описать взаимные изменения переменных величин, характеризующих изучаемые процессы, т. е. в конечном итоге найти одни переменные как функции других. В большом числе практических случаев интересуются изменением переменных величин во времени. При этом важнейшей характеристикой, определяющей поведение переменной величины во времени, является быстрота ее изменения.

Если некоторая зависящая от времени переменная величина и (t) в момент времени tj имела значение а в момент времени /г получила новое значение иг (рис. 22-10), то говорят, что переменная величина и получила приращение Аи = иг - i за приращение времени Д<=(2-fj. Здесь Д означает символ приращения. Отношение приращения функции к приращению ее аргумента Д

- равно средней скорости изменения функции ы (О в интервале времени - i- Чем меньше интервал изменения аргумента Д^, тем ближе значение средней скорости к истинной скорости в момент t. Если интервал Д^ в процессе уменьшения стремится

к нулю (Д<->- 0), то отношение - стремится к некото-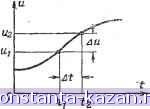

Рис. 22-10.

рому предельному значению, которое точно равно скорости изменения переменной величины и называется производной переменной величины и (t) по независимой переменной t

Производная яв'ляется количественной мерой приращения переменной величины.

Операция нахождения производной сводится к вычислению указанного выше предела. Она производится

§ 22-8]

Математическое списание физических процессов

по специальным правилам и обозначается следующим образом:

du ,. Дм

--vt = Iim -гт, dt ht

Д?->0

где lim (предел) означает нахождение предела.

Производные переменных величин сами могут быть функциями времени. Поэтому можно определить производную от производной, т. е, вторую производную:

Вторая .производная является ускорением переменной величины.

Аналогичным образом определяются и высшие производные.

Примеры

1. Напряжение на катушке индуктивности при протекании через нее тока пропорционально скорости его изменения (постоянный ток падения напряжения на индуктивности не создает):

2. Ток, протекающий через конденсатор, пропорционален скорости изменения напряжения на его обкладках:

с(0 = С

dt

Дифференциальные уравнения

Описать математически тот или иной физический процесс, -изменяюцщйся во времени, это значит установить связь между производными, характеризующими быстррту изменения переменных величин.

Математическое соотношение, связывающее неизвестную функцию и ее производные по одной независимой переменной величине, называется обыкновенным дифференциальным уравнением.

Пример. Требуется составить дифференциальное уравнение заряда конденсатора (рис. 22-П).

£

Рнс. 22-U.

Введем следующие обозначения: Е - напряжение внешнего источника; R - сопротивление цепи; С - емкость конденсатора; i - ток в цепи; ис - напряжение иа емкости.

Тогда ток в цепи

падение напряжения на сопротивлении

Пользуясь вторым законом Кирхгофа можно напи-£ = i?C -Ь С или £ = RCDuc -f ис.

символ операции нахождения произ-

где D - условный водной, =

Полученное уравнение описывает процесс заряда конденсатора от источника постоянного напряжения.

Порядком дифференциального уравнения называется порядок наивысшей из производных, входящих в это уравнение.

Решить дифференциальное уравнение - это значит найти входящую в негб переменную как явную функцию времени. Решение дифференциального уравнения не содержит производных.

Пример. Решение дифференциального уравнения заряда конденсатора имеет вид

С

= £(l .

где е SS 2,718 - основание натуральных логарифмов.

Процессы в сложных системах, поведение которых характеризуется многими переменными величинами, описываются системами дифференциальных уравнений.

Система дифференциальных уравнений считается решенной, если все переменные определены как функции времени.

Обыкновенное дифференциальное уравнение порядка п записывается в следующей форме:

или

CoD X -f щВ ~х -h .. . -ha-iDx + a x = f (/).

Если коэффициенты уравнения Qj являются постояН: ными, то мы имеем дифференциальное уравнение с постоянными коэффициентами.

Дифференциальное уравнение, коэффициенты которого являются функциями времени t, называется дифференциальным уравнением с переменными коэффициентами.

Дифференциальное уравнение, коэффициенты которого зависят от искомой функции, называется нелинейным дифференциальным уравнением.

Для получения вполне определенного решения дифференциального уравнения или системы, учитывающего начальное состояние исследуемого процесса, необходимо знать начальные условия, т. е. значения входящих в уравнение переменных и их производных в начальный момент времени. Число необходимых начальных условий равно порядку дифференциального уравнения. Например, для определения процесса изменения напряжения на конденсаторе важно знать, был ли он заряжен и до какого напряжения к моменту включения внешнего источника напряжения.

Интеграл

Если известна скорость изменения переменной вели-

чины м (Q, т. е. производная у = -,то полное изменение

величины и (f) за промежуток времени т tg до t можно приближенно определить как сумму элементарных приращений переменной на всех достаточно малы.\ интерва-