лах А и == ij-fi - и, составляющих весь промежуток t~ tg.

Значение производной внутри каждого интервала Д ti принимается постоянным и равным ее значению в середине

п

интервала. В результате получится сумма 2 U-t.

1=0

(рис. 22-12), где 2 обозначает операцию суммирования.

Пример. Ток, протекающий через емкость С под действием переменного напряжения Uc (О, равен:

.с(0 = с^.

Учитывая связь между интегралом и производной, можно записать:

с(0 =

ic{t)dt.

to t, tz t3

Рис. 22-12.

Предел полученной суммы при условии, что каждый интервал Д</ стремится к нулю (Д^- 0), а количество п таких интервалов на промежутке / - tg стремится к бесконечности (п оэ), называется интегралом функции у (t) за время t - tgK обозначается следующим образом:

22-9. ПРЕДСТАВЛЕНИЕ МАТЕМАТИЧЕСКОЙ ЗАДАЧИ В ВИДЕ БЛОК-СХЕМЫ

Блок-схема решения уравнения

Любая задача, решаемая на моделирующей установке, представляется в виде определенных соотношений между переменными, которые набираются на моделирующей установке.

Перед набором задачи необходимо представить ее в виде блок-схемы, которая позволяет определить количество и типы решающих элементов, их параметры и характер взаимных связей между ними.

Пусть, например, искомая величина х связана с величиной у следующим соотношением:

х = у -\- ау.

y{t)dt= Пш 2wA/.

/г->оо

Символ J называется знаком интеграла; число tg -нижним пределом; число t - верхним пределом; функция г/(Q - подынтегральной функцией; выражение у (t) dt - подынтегральным выражением; буква t - переменной интегрирования.

Геометрически интеграл представляет собою площадь фигуры, ограниченной осью абсцисс, прямыми, параллельными оси ординат и проходящими через абсциссы ig и t, и графиком функции у (t).

Если верхний предел представляет собой конечное число t= ti, то интеграл имеет конечное значение; если верхний предел переменный, то интеграл является функцией верхнего предела. В этом случае интеграл имеет производную по верхнему пределу.

Между интегралом с переменным верхним пределом и его производной существует однозначная зависимость.

=J y{r)dx, то 5F = W-

Таким образом, если процесс дифференцирования (нахождения производной) позволяет по известной функции найти скорость ее изменения, то процесс интегрирования позволяет по известной скорости изменения функции найти саму функцию.

Иными словами, интегрирование есть действие, обратное дифференцированию.

Для обозначения интегрирования используется символическая запись:

ауг

Сложение

Выход

Рис. 22-13.

Процесс решения этой задачи может быть представлен в виде блок-схемы, показанной на рис. 22-13.

Если решающие элементы не позволяют производить умножение на а > 1, то уравнение преобразуется к виду

и решение выполняется по блок-схеме, приведенной на рис. 22-14.

Умножение

ВсзвеВение в квадрат

y[{)dt=-Ly({).

, Рис. 22-14.

В результате решения получается искомая величина х, уменьшенная в а раз.

Если искомая величина х является функцией нескольких переменных у, г, д . . ., например

X у + yz + sin д.

§ 22-9]

Представление математической задачи в виде блок-схемы

Умножение

Сложение

Рис. 22-15.

то схема решения задачи имеет несколько входов. Результаты операций над переменными смешиваются и осуществляют правильную зависимость (рис. 22-15),

Блок-схема решения системы уравнений

Если задана для решения система нескольких уравнений, например

х = у+ ах; у = х-\- Ьу,

то каждое уравнение решается электрически для своей переменной с помощью группы решающих элементов. Результат решения подается на вход следующей группы решающих элементов, на которой набрано другое уравнение системы, и т. д. (рис. 22-16).

Схема решения уравнения х=у+ах

Рис. 22-16.

Возведение в неадрат

Умножение на а

Обратная связь

схему решения. Для избежания этой трудности необходимо рассматривать величину х, стоящую в правой части уравнения, как известную, ибо она должна получаться на выходе группы решающих элементов. Эту величину следует подать на вход схемы, образовав, таким образом, заданное математическое соотношение. В результате получится блок-схема решения, показанная на рис. 22-17.

Как в случае решения системы уравнений, так и в случае использования метода неявных функций блок-с;сема решения содержит обратные связи.

В каждом конкретном случае необходимо принимать меры, чтобы избежать образования положительных обратных связей, могуцщх привести к неустойчивости схемы решения уравнения.

Блок-схема решения дифференциального уравнения

Так как дифференциальное уравнение содержит производные искомой величины, зависящей от времени, то для нахождения этой величины необходимо выполнить действие интегрирования. Поэтому для решения дифференциального уравнения на модели необходимо иметь решающие элементы, называемые интеграторами.

Электронные моделирующие установки, на которых можно решать дифференциальные уравнения, часто называют электронными интеграторами.

Количество интеграторов, необходимых для решения уравнения, равно порядку последнего.

При решении дифференциальных уравнений иа модели используется метод неявных функций, а именно, принимается, что искомая функция и все ее производные, кроме старшей, известны. Тогда сумма всех этих величин, при-

J Интегрирование

duc dt

!/множение

Интегрирование

о-с

Умнстение

Установленные таким образом взаимные связи между группами решающих элементов позволяют получить решение, удовлетворяющее одновременно всем уравнениям системы.

Блок-схема решения задачи методом неявных функций

В уравнениях, подобных одному из уравнений рассмотренной выше системы х = у+ а>?, величину х невозможно выразить в явном виде, чтобы составить блок-

Сло^ение

?>ис. 22-18. Блок-схема решения дифференциального уравнения колебательного контура.

нятых известными и умноженных на коэффициенты, определяемые уравнением, даст значение наивысшей производной. Интегрируя эту сумму, можно получить производную меньшего на единицу порядка и подать ее на вход схемы. Интегрирование производится последовательно столько раз, каков порядок уравнения, и выход каждого интегратора подается на вход схемы решения с коэффициентом и знаком, определяемыми структурой уравнения. Переменная величина на выходе последнего интегратора является искомой функцией времени.

Например, дифференциальное уравнение, определяющее изменение напряжения на емкости ис последователв-ного контура, состоящего из индуктивности L, сопротивления R и емкости С, при включении -а , на вход постоянного напряжения Е имеет следующий вид;

duc R due i J <Й2 + z, (й'

uc =

Рис. 22-п.

и может быть решено с помощью схемы, содержащей два интегратора (рис. 22-18).

Схема для решения дифференциального уравнения в большинстве случаев имеет обратные связи.

Решение систем дифференциальных уравнений выполняется по методу, описанному выше (рис. 22-16).

При решении дифференциальных уравнений обязательно вводятся начальные условия.

Типы основных решающих элементов

Сложные математические задачи можно решить с помощью комбинаций ограниченного числа простых операций, выполняемых основными решающими элементами.

На практике широкий круг задач решается путем комбинаций следующих решающих элементов:

1) устройства для получения суммы двух или нескольких величин;

2) устройства для умножения переменных величин на постоянный коэффициент;

3) устройства для изменения знака переменных величин;

4) устройства для образования произведения двух переменных величин;

5) устройства для образования различных функций переменных величин;

6) устройства для получения интеграла от изменяющихся во времени переменных величин;

7) устройства для умножения переменных величин на коэффициент, изменяющийся во времени.

Приведенный перечень решающих элементов позволяет составить схемы для решений обыкновенных дифференциальных уравнений трех указанных типов (линейных с постоянными и переменными коэффициентами и нелинейных), а также систем дифференциальных уравнений.

Представление переменных величин в электронной модели

Физические величины, входящие в систему решаемых уравнений, представляются в электронной модели напряжениями. Эти напряжения носят название машинных переменных. Таким образом, с помощью электронной модели устанавливаются математические зависимости не между исходными переменными решаемой задачи, а между машинными переменными. Для того чтобы отразить это различие, принято исходные переменные обозначать малыми буквами, а машинные - заглавными.

В электронных моделях, выпускаемых в Советском Союзе, машинные переменные изменяются в пределах ± 100 в, поэтому за единицу их измерения принимают машинную единицу, равную ста вольтам.

22-10. ПРИНЦИПЫ ИСПОЛЬЗОВАНИЯ ЭЛЕКТРИ ЧЕСКИ.Х ЦЕПЕЙ ДЛЯ ВЫПОЛНЕНИЯ МАТЕтАТИЧЕСКИХ ОПЕРАЦИЙ

Умножение на постоянный коэффициент

Для умножения на постоянный коэффициент используют делитель напряжения или линейный потенциометр, если величина постоянного коэффициента К заключена между нулем и единицей.

Для делителя или потенциометра (рис. 22-19, а) справедливо соотношение

где/Cf-

Значение установленного коэффициента может бьггь прочитано по шкале потенциометра, градуировка которой будет линейной, если нагрузка, включенная на выход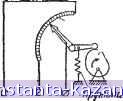

Потенциометр

Вход Выход б)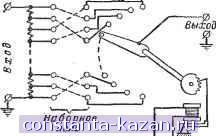

Шаговый двигатель

л, л...... Импульсы

напрйтения

Рис. 22-19. Делитель напряжения (о), кулачковый вариатор коэффициентов (б) и вариатор коэффициентов с шаговым искателем (в).

потенциометра, очень мала, а источник входного напряжения обладает достаточной мощностью.

Если потенциометр нагружен на конечное сопротивление i?h, то

где

/Ci = A-

\ + К{1-К)§-

Влияние нагрузки приводит к зависимости kosiJ циента передачи цепи от величины нагрузки и от произведения плеч потеншюметра. Влияние нагрузки уменьшается с увеличением

Умножение на по)еменный коэффициент

Устройства, предназначенные для реализации переменных во времени коэффициентов, называются вариаторами коэффициентов или блоками переменных коэффициентов. Используются электромеханические и электронные вариаторы коэффициентов.

Электромеханический вариатор представляет собой линейный потенциометр или делитель напряжения, положение движка (отвода) которого изменяется в соответствии с заданной для воспроизведения функцией времени (рис. 22-19, б и е). На вход такого устройства подается напряжение, которое надлежит умножить на переменный во времени коэффициент. Основным элементом, с помощью которого изменяется положение отвода потенциометра, является профилированный кулачок, выполненный в соответствии с заданной для воспроизведения функцией времени, или шаговый искатель с большим количеством ламе-лей.

При необходимости получения переменных коэффициентов с большой скоростью изменения используются электронные вариаторы (см. стр. 482).