поступающее на вход четырехполюсника, называется воздействием. Напряжение Uif), получаемое при этом на выходе четырехполюсника, называется откликом.

Различия в линейных радиотехнических цепях заключаются главным образом в соотношениях между воздействием и откликом.

Цепи, предназначенные для неискаженной передачи электрических возмущений, называются линиями. В них отклик должен по возможности точно повторять воздействие.

В усилителях также стремятся избежать искажений формы воздействия, но отклик должен превышать воздействия по мощности (или по амплитуде). Необходимая для этого дополнительная мощность доставляется источниками питания.

Рис. 4-22. Схема четырехполюсника.

Однако далеко не всегда отклик должен повторять воздействие. Иногда, например, требуется устранить некоторые частоты из спектра воздействия. Эту функцию выполняют фильтры. В других случаях может потребоваться определенное запаздывание отклика по сравнению с воздействием; это осуществляется в линиях задержки. Может потребоваться накопление воздействия Б так называемой интегрирующей цепи или получение отклика, пропорционального скорости изменения воздействия, в так называемой дифференцирующей цепи и т. д.

Отклик линейной цепи зависит как от воздействия, так и от свойств цепи. В соответствии с частотными и временными представлениями сигнала (см. § 4-1) свойства линейных радиотехнических цепей могут описываться частотными характеристиками и временными характеристиками.

Коэффициент передачи

Частотной характеристикой радиотехнической цепи называется коэффициент передачи, представляющий собой отношение комплексной амплитуды отклика к комплексной амплитуде воздействия:

Реальный сигнал, воздействующий ка радиотехническую цепь, состоит из ряда синусоидальных составляющих. Зная эти составляющие воздействия и коэффициент передачи для каждой из частот передаваемого спектра, легко найти все составляющие отклика:

и2 = К (со) йг.

Отсюда, в частности, следует простое соотношение между спектральными плотностями отклика и воздействия;

Фг (<о)= i<:(<o)Oi((o),

т. е. спектр отклика Фа (ш) равен спектру воздействия Фт (ш), умноженному на коэффициент передачи. Иллюстрацией к этому правилу является преобразование спектра воздействия с помощью полосового фильтра, коэффициент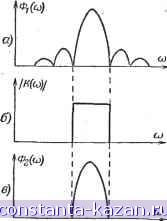

Рис. 4-23. Спектр воздействия (а), амплитудно-частотная характеристика фильтра (б) и спектр отклика (в).

передачи которого отличен от нуля лишь в полосе F передаваемых частот (рис. 4-23).

Коэффициент передачи представляет собой комплексную величину:

а{<о) = Л(щ)

Модуль коэффициента передачи равен отношению действительных амплитуд отклика и воздействия

иназывается амплитудно-частотной характеристикой цепи.

Аргумент коэффициента передачи ф (to) выражает фазовый сдвиг между синусоидальными напряжениями на выходе и входе цепи и называется фазово-частот-ной характеристикой.

Переходная функция

Временной характеристикой радиотехнической цепи является переходная функция. Для ее определения представим, что до некоторого момента времени ни- s(t) какого воздействия на цепь не 7 было, а затем на вход цепи подано напряжение, равное еди-

нице, которое в дальнейшем не о изменяется,

0(0 = 1.

6(t-r)

Такое воздействие называется единичной функцией или функцией включения (рис. 4-24).

Отклик цепи на воздействие в виде единичной функции называется переходной функцией h (t).

Переходная функция представляет особые удобства для анализа процессов, протекающих во времени, ц, в частности, переходных процессов. Любое

Рис. 4-24. Единичная функция без запаздывания (а) и с запаздыванием (б).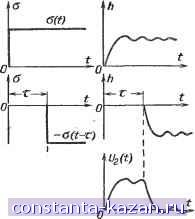

Модуль этого сопротивления

Рис. 4-25. Использование переходной функции для определения переходного процесса, вызываемого прямоугольным импульсом.

сложное воздействие на электрическую цепь можно представить в виде суммы единичных функции. Зиая отклик системы на единичную функцию, можно таким путем найти отклик на воздействие любой сложности. В качестве иллюстрации на рис. 4-25 показан путь нахождения переходного процесса в цепи, на которую действует прямоугольный импульс, представленный суммой двух единичных функций.

Последовательный колебательный коитур

Сдвиг фаз между э. д. с. источника и током в контуре определяется из соотношения

coL -

R

Наименьшим сопротивлением

мин ~ R

последовательный контур обладает при

coL =

т. е. при совпадении частоты источника колебании (или несущей частоты принимаемого сигнала) с частотой сОр свободных колебании в контуре.

со = СОп =

V LC

Этот случай носит название резонанса, а частота со = СОр называется резонансной частотой. При резонансе в последовательном контуре могут быть замечены следующие явления:

1) индуктивное сопротивление контура компенсируется численно равным, но противоположным по знаку емкостным сопротивлением;

Колебате;ьньш контуром называется цепь, состоящая из последовательно соединенных конденсатора С, катушки индуктивности L и сопротивления R. Чтобы в контуре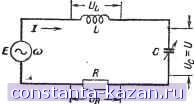

Рис. 4-26. Последовательный колебательный контур.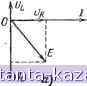

Рис. 4-27. Векторные диаграммы напряжений в последовательном контуре при частотах ниже резонансной (а), резонансной (б) - и выше резонансной {в).

имели место незатухающие вынужденные колебания, необходимо питать его от источника колебаний, который может быть включен последовательно (рис. 4-26) или параллельно (см. рис. 4-30) обоим реактивным элементам.

Последовательное включение применяется для источников с малым внутренним сопротивлением. Включая последнее в R, получим полное сопротивление цепи последовательного контура:

Z=i- = R+j[.L-l.

2) ток Б контуре становится наибольшим;

3) ток Б контуре совпадает по фазе с э. д. с. источника (Ф=0);

4) приложенная к контуру э. д. с. целиком падает на активном сопротивлении, так как напряжения на реактивных элементах компенсируют друг друга. Благодаря этому резонанс в последовательном контуре называется резонансом напряжений.

Сказанное хорошо иллюстрируется векторными диаграммами напряжении на элементах последовательного контура (рис. 4-27).

Настройка последовательного контура в резонанс с несущей частотой принимаемого сигнала производится

конденсатором переменной емкости. С этого же конденсатора обычно снимается выходное напряжение:

соС \Z\ шС

(02 \ 2 щ2 ;j2C

1:--2

Графическое изображение амплитудно-частотной характеристики контура называется резонансной кривой. Семейство резонансных кривых для различных затуханий контура d представлено на рис. 4-28 Чем меньше затухание контура, тем более острую вершину и крутые скаты имеет резонансная кривая.

При настройке контура в резонанс с частотой источника колебаний получаем:

я макс J

макс - Е- - л

Величину, обратную затуханию, называют добротностью контура:

ЮО 90 80 70 60 50 40 30

В современных радиотехнических контурах эта величина может быть порядка 200-300. Добротность контура показывает, во сколько раз резонансное значение напряжения на реактивном элементе превышает э. д. с, приложенную к контуру

0,2 0,1 О 0,1 Q2

Рис. 4-28. Резонансная характеристика колебательного контура.

Расстройкой контура называют разность между резонансной частотой и частотой колебаний:

В таком случае для частот, близких к резонансной ш яа щ, величину

Острая резонансная характеристика позволяет путем настройки контура в резонанс с несущей частотой сигнала осуществить селекцию полезного сигнала, т. е. выделение его из множества других сигналов, которые имеют другую частоту, попадают на скат резонансной кривой и ослабляются по сравнению с полезным сигналом.

Но ослабляя сигналы соседних радиоканалов, контур должен пропускать без заметного ослабления все составляющие спектра полезного сигнала. Для этого контур должен обладать достаточно широкой полосой пропускания 2Др(1) (рис. 4-29), которую принято определять на уровне

. Л = = 0.707 акс.

(1)2 tpZ (Щд -{- (0) ((О (Дд) 2Дсй 6- -о~ 1 - ~ 2-- 2

естественно называть относительной расстройкой.

Затуханием контура принято называть величину

R R

где

tOoC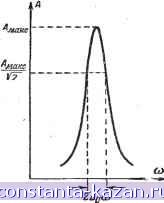

называется характеристическим сопротивлением контура.

Используя эти обозначения, получим выражение для амплитудно-частотной характеристики контура, пригодное для частот, близких к резонансной

Л. -

Рис. 4-29. Определение полосы пропускания контура.

Ширина полосы пропускания контура может быть легко найдена из условия

Л1 JfiKUn I