§ 4-3]

Воздействие сигнала на линейные радиотехнические цепи -if-----

Одиночный контур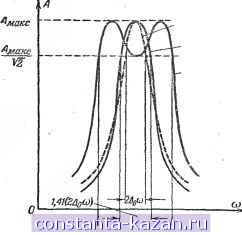

на котором определяется ширина пропускания.

Рнс. 4-35, Определение полосы пропускания двух одинаковых связанных контуров.

Но уже при критической связи (й^в. кр = 2АоШсв. кр = 1.41 (2АоСО).

При дальнейшем увеличении связи полоса расширяется, но равномерность пропускания частот ухудшается, так как на резонансной кривой появляется впадина. Такая впадина считается допустимой вплоть до уровня

Этот предельный случай соответствует коэффициенту связи Асв = 2,4 Ы и полосе пропускания

2АоШсв. макс = 3,1 (2ДоШ).

Дальнейшее расширение полосы нецелесообразно из-за большого ослабления средних частот спектра.

Значительная ширина полосы пропускания и крутые скаты резонансной кривой связанных контуров свидетельствуют о том, что связанные контуры обладают значительно более благоприятными избирательными свойствами по сравнению с одиночным контуром (рис. 4-35).

Резонанс на частотах связи соответствует максимуму тока /j в первом контуре. Но практически гораздо более важно настроить контуры так, чтобы получить наибольший ток /г во втором контуре. При неизменных частоте ш. и напряжении Е источника колебаний это можно сделать тремя способами: 1) изменением реактивностей первого контура; 2) изменением реактивностей второго контура и 3) изменением степени связи между контурами. В зависимости от порядка использования этих способов (или их комбинаций) возможны чагыре случая настройки связанных контуров на максимум тока во втором контуре (табл. 4-8).

Частные резонансы позволяют получить максимальные значения тока I.m, но не наибольшие из возможных значений. Наибольшее из всех возможных значений тока во втором контуре /gmm дает сложный резонанс и полный резонанс. Оптимальной

Таблица 4-S

Наименование способа получения максимального тока во втором контуре

Порядок настройки связанных контуров

Условие максимума тока во втором контуре

Величина тока во втором и первом контурах

Первый частный резонанс

Настройка (изменение емкости или индуктивности) первого контура

1чт\ -

1 - Jml

Второй частный резонанс

Настройка (изменение емкости или индуктивности) второго контура

7i = /-2mII

I 2, I

Сложный резонанс

Настройка одного из контуров и подбор оптимальной связи между контурами. Например, выполняют условие первого частного резонанса, а затем увеличивают связь, дополнительно подстраивая первый контур (настройку другого контура не меняют)

\\ XL

(достаточно выполнения двух из этих равенств)

2тт -

2 YRR В 2R

Полный резонанс

Настройка на частоту генератора каждого из контуров в отдельности и подбор оптимальной связи между контурами

Xi = 0; Х2 = 0;

X=YRrR2

-гтт -

2 Y RiR-2 Е

связью при осуществлении полного резонанса является критическая связь

*св. кр -

При критической связи значение Imm достигается на одной частоте. При связи, большей критической, получение /jmm возможно на двух частотах (частотах связи). При связи, меньшей критической, получение Imm невозможно.

Фильтры

Электрическим фильтром называется устройство, пропускающее колебания одних частот с небольшим ослаблением, а колебания других частот - с большим ослаблением. Частоты колебаний, пропускаемых фильтром без большого ослабления, образуют п о-лосу прозрачности (пропускания) фильтра. Частоты колебаний, задерживаемых фильтром, образуют полосу непрозрачности (непропускания). Частота, лежащая на границе этих полос, называется частотой среза fc-

В зависимости от расположения полосы прозрачности на шкале частот различают:

1) фильтры нижних частот, пропускающие без большого ослабления колебания всех частот ниже некоторой частоты среза f,

2).фильтры верхних частот, пропускающие без большого ослабления колебания всех частот выше некоторой частоты среза f,

3) полосовые фильтры, пропускающие без большого ослабления колебания определенной полосы частот от до

4) заграждающие фильтры, сильно ослабляющие колебания определенной полосы частот от /с1 ДО hi-

Ослабление фильтром напряжения (или тока) оценивают отношением амплитуды напряжения на входе к амплитуде Uz напряжения на выходе. Обычно это отношение выражают в децибелах:

b=2oig- т

и называют затуханием фильтра (не путать с затуханием колебательного контура!).

Зависимость затухания фильтра от частоты называют частотной характеристикой затухания фильтра.

Простейшими фильтрами являются обычные реактивные сопротивления и их соединения. Например, падение .напряжения на катушке индуктивности тем меньше, чем меньше частота, а на конденсаторе, наоборот, тем меньше, чем больше частота. Таким образом, последовательно включенная в цепь катушка индуктивности может служить фильтром нижних частот, а последовательно включенный конденсатор - фильтром верхних частот. Резонансные явления Б последовательном и параллельном колебательных контурах позволяют использовать их в качестве полосовых или заграждающих фильтров (в зависимости от включения контура). Однако все эти цепи не позволяют достигнуть резкого разграничения пропускаемых и задерживаемых частот. Несколько лучшие результаты могут быть получены при использовании связанных контуров в качестве полосовых фильтров.

Значительно более высокими показателями обладают фильтры в виде четырехполюсников, которые составлены из реактивных сопротивлений, соединенных б виде Г-образных, Т-образкых или П-образных звеньев (рис. 4-36).

2,/2

1-1-

-9 Ф

Рис. 4-36. Схемы звеньев электрических фильтров: а - Г-образное звено; б - Т-образное звено; в - П-образное звено.

Если произведение последовательно и параллельно включенных реактивных сопротивлений этих звеньев не зависит от частоты

{К - постоянная величина), то такие фильтры называются фильтрами типа К. Условием, определяющим полосу прозрачности этих фильтров, является неравенство

в табл. 4-9 приведены схемы и частотные характеристики затухания Т-образных и П-образных звеньев фильтров типа К-

Возрастание затухания при со > в фильтрах нижних частот объясняется увеличением сопротивления последовательных индуктивных ветвей и уменьшением сопротивления параллельных емкостных ветвей.

Возрастание затухания при со < (0. в фильтрах верхних частот объясняется увеличением сопротивления последовательных емкостных ветвей и уменьшением сопротивления параллельных индуктивных ветвей.

ii-M)z,

Рис. 4-37. Образование фильтра типа М (б) из фильтра типа К (с).

Возрастание затухания за пределами полосы прозрачности полосовых фильтров объясняется увеличением сопротивления последовательного контура и уменьшением сопротивления параллельного контура по мере удаления от резонансной частоты этих контуров, находящейся в пределах полосы прозрачности.

Возрастание затухания в пределах полосы непрозрачности заграждающих фильтров объясняется увеличением сопротивления параллельного контура и уменьшением сопротивления последовательного контура по мере приближения к резонансной частоте этих контуров, находящейся в пределах полосы непрозрачности.

Недостатками фильтров типа К являются: 1) малая крутизна частотных характеристик затухания; 2) трудность согласования фильтра с источником колебаний и с нагрузкой. Освободиться от этих недостатков позволяет перераспределение реактивных сопротивлении в последовательных и параллельных ветвях звеньев фильтра. Например, в последовательных ветвях фильтра нижних частот оставляют лишь М-к> часть индуктивности

Таблица 4-9

Наименование фильтра

Схема Т-образного и П-образвого звеньев фильтра

Частотная характеристика фильтра

Частоты среза

Фильтр нижних частот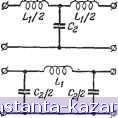

Фильтр верхних частот

-il-0

0- I i-0

2 VL,C,

Полосовой фильтр

-г

с1 = о (Ti + т~-т); С0с2 = о (yi + m-l- m),

где m = -т- =

C2 1

Заграждающий фильтр

о о о

-с

Частоты среза вычисляются так же, как и в случае полосового фильтра

а остальную индуктивность переносят в параллельную ветвь (рис. 4-37). В результате этого в параллельной ветви фильтра образуется последовательный контур. По мере приближения к резонансной частоте cOq этого контура шунтирующее действие параллельной ветви фильтра возрастает, что вызывает увеличение крутизны частотной характеристики затухания. При резонансе в параллельной ветви фильтр оказывается закороченным и его затухание становится бесконечно большим. Это позволяет значительно улучшить крутизну частотной характеристики затухания фильтра (рис. 4-38). Одновре-

менно обеспечивается лучшее согласование фильтра с нагрузочным сопротивлением.

Характеристики подобных фильтров зависят от расчетного параметра Af. Поэтому эти фильтры названы фильтрами типа М. Поскольку произведение общей индуктивности и емкости при переходе от фильтра типа К к фильтру типа М остается неизменным, то частоты среза и полоса прозрачности у фильтров обоих типов одинаковы.

Другим способом увеличения крутизны частотной характеристики затухания фильтра является увеличение