числа его звеньев. Обычно фильтр строится из звеньев с одинаковой полосой прозрачности. Чем больше число звеньев фильтра, тем больше приближение к характеристике идеального фильтра, которая имеет бесконечную крутизну на границе полосы прозрачности и бесконечно большое затухание в полосе непрозрачности.

Полосовые фильтры типов Kw.M рассчитываются обычно на полосы пропускания не менее нескольких процентов от средней частоты. Более узкие полосы пропускания, составляющие десятые доли процента от средней частоты.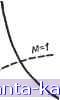

Рис. 4-38. Частотная характеристика затухания фильтра нижних частот при М = 1 а М = 0,6.

могут быть получены лишь в электромеханических фильтрах (пьезоэлектрических или магнито-стрикциоиных), действие которых основано иа преобразовании электрической энергии в механическую и обратно.

Наибольшее распространение получили кварцевые фильтры. Явление пьезоэлектричества, наблюдаемое в кристалле кварца, заключается в том, что при механическом сжатии кристалл электрически поляризуется (см. § 3-1), и, наоборот, при приложении к граням кристалла электрического напряжения происходит механическая деформация кристалла. Пластинка кварца, помещенная в переменное электрическое поле, совершает механические колебания с частотой изменения поля. При совпадении частоты собственных механических колебании пластины и частоты электрического поля наступает резонанс, характеризуюшдйся наибольшими амплитудами механических и электрических колебаний. Резонансная частота кварцевой пластинки Д, зависит лишь от толщины пластинки й:

2 h

где /о - в мегагерцах; h - в миллиметрах.

Обладая резонансными свойствами, кварцевая пластинка оказывается эквивалентной сложному колебательному контуру третьего вида с очень высокой добротностью (порядка нескольких тысяч) и узкой полосой пропускания (0,2-0,4%). Это и послужило причиной использования кварцевых пластин в качестве составных элементов сложных фильтров с высокими качественными показателями.

ключении активных или реактивных сопротивлении к участкам таких цепей, на которых имеет место падение напряжения. Переходные процессы всегда связаны с изменением общего запаса энергии в электрической цепи. Как только общий запас энергии прекращает изменяться, переходный процесс заканчивается.

Физической причиной возникновения переходных процессов является невозможность мгновенного изменения электрической и магнитной энергии, запасенной в конденсаторах и катушках индуктивности. Известно, что при подключении к источнику постоянного напряжения ток в катушке индуктивности и напряжение на обкладках конденсатора устанавливаются не скачком, а постепенно изменяясь от нуля до максимального значения. Аналогично этому колебания в последовательном (или параллельном) контуре LCR при подключении его к источнику колебаний Е и при отключении его от этого источника не возникают и не исчезают скачком, а нарастают и убывают постепенно (рис. 4-39).

Переходный процесс, возникающий после включения источника колебании, является результатом сложения вынужденных колебаний (колебаний установившегося режима) и затухающих свободных колебаний, возникаюших в контуре в момент включения. Если контур имеет некоторую расстройку, то из-за различия частот вынужденных и свободных колебаний возникают биения и огибающая переходного процесса после включения претерпевает колебания (рис. 4-39, а). Если же контур точно настроен на частоту источника колебании, то амплитуда колебании в контуре нарастает монотонно (рис. 4-39, б).

По прошествии времени Л свободные колебания затухают и в контуре происходят установившиеся колебания постоянной амплитуды.

После отключения источника колебаний от контура Б последнем вновь возникают свободные колебания за

а Фс

jficc после I ключенип I I

Рис. 4-39, Переходный процесс в расстроенном (а) и настроенном (б) колебательном контуре.

Переходные процессы в линейных цепях

Процессы перехода от одного установившегося состояния электрической цепи к другому называются переходными процессами. Они наблюдаются при включении источников колебаний в цепь, содержащую индуктивности и емкости, при отключении источников колебаний от таких цепей, а также при под-

счет энергии, накопленной при установившемся режиме. По прошествии времени Д^2 эти свободные колебания затухают.

Таким образом, длительность переходного процесса в колебательном контуре определяется длительностью существования в нем свободных колебаний. Теоретически свободные колебания затухают до нуля лишь через бесконечно большой промежуток времени. Но практически

�03176055265

с ними можно не считаться, если их амплитуда падает до нескольких процентов, например, до 5% от первоначальной амплитуды. Это происходит через время

т. е. длительность переходного процесса обратно пропорциональна полосе пропускания контура. Чем выше добротность контура, тем больше длительность переходного процесса. Для сокращения длительности переходных процессов приходится увеличивать затухание контура.

а) о

б) о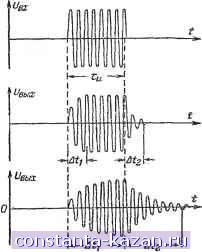

Рис. 4-4G. Искажение прямоугольного импульса при прохождении его через колебательный контур.

При прохождении высокочастотных импульсов через колебательный контур форма импульса может сильно исказиться из-за переходных процессов (рис. 4-40). Считая, что нельзя допускать большие искажения, чем те, которые изображены на рис. 4-40, в, получим:

т„.

Таким образом, для пропускания импульса длительностью Ти необходимо выбирать полосу пропускания

Обычно выбирают

2AJ =

в зависимости от допусти?.1ых искажений импульса.

Цепи с распределенными параметрами

Все рассмотренные ранее линейные цепи относились к цепям с сосредоточенными пара-мет-рами. В них с достаточным для практики при-блшкением можно считать, что все электрическое поле сосредоточено только в конденсаторе, магнитное поле - в катушке самоиндукции, а активные потери происходят только в тех местах, где включено активное сопротивление.

В соответствии с этим можно принять, что вся емкость такой цепи сосредоточена в конденсаторе, а индуктивность - в катушке самоиндукции. Активное сопротивление можно считать включенным лишь на отдельных участках цепи, а все соединительные провода - идеально проводящими.

Но такая картина является лишь некоторым приближением к действительности, так как в общем случае электрические и магнитные поля цепи, а также области активных потерь не разделены пространственно, и поэтому индуктивность, емкость и активное сопротивление (проводимость) распределены по цепи. В случаях, когда упрощающее представление о сосредоточенных параметрах цепи ведет к большим искажениям физической картины явлений и, следовательно, к ошибочным выводам, говорят о цепях с распределенными параметрами.

Цепи с распределенными параметрами встречаются в виде линий и фидеров (двухпроводных, четырехпровод-ных, коаксиальных), волноводов, объемных резонаторов и антенн. На любом участке этих цепей имеются активное и индуктивное сопротивления проводов, а также емкостная н активная проводимости между проводами.

Двухпроводная линия

Рассмотрим линию, состоящую из двух параллельных проводов, которые на любом участке длиной I обладают одинаковыми погонными параметрами.

I , -1- / - / r I

Полное погонное сопротивление и полная погонная проводимость линии:

2i = + /caii: Fj = Gj -f / >Ci.

В радиотехнических двухпроводных линиях часто можно пренебречь потерями и считать

= 0; Gi = 0.

Такая идеальная линия состоит лишь из распределенных последовательных индуктивностей и распределенных параллельных емкостей (рис. 4-41). Если в начале

22 X

2г

Рис. 4-41. Двухпроводная линия (с) и ее эквивалентная

схема (б). J

линии включить источник постоянного напряжения Uq, то емкость С заряжается источником Ug через индуктивность L, затем емкость С заряжается емкостью С' через индуктивность L , емкость С заряжается емкостью С и т. д. Последовательный заряд распределенных емкостей через распределенные индуктивности создает волну тока и напряжения. Эта волна движется со скоростью v от источника напряжения к нагрузке и поэтому называется падающей волной.

Если нагрузка не может полностью поглотить энергию, доставляемую к концу линии падающей волной,

A99C

2395

то возникает отраженная волна, которая также представляет собой последовательный разряд (или заряд) распределенных емкостей через распределенные индуктивности. В результате через любое сечение линии проходят две волны тока н напряжения: падающая и отраженная.

В том случае, если в начале линии включен источник синусоидального напряжения с частотою со = 2nf:

U=Uo cos at,

то падающая и отраженная волны представляют собой процесс последовательной перезарядки распределенных емкостей через распределенные индуктивности. При этом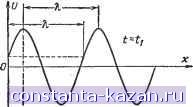

Рис. 4-42. Перемещение падающей волны напряжения вдоль линии.

напряжение и ток в любом сечении х линии изменяются во времени синусоидально (т. е. повторяют закон изменения напряжения источника), но это изменение отстает от изменений напряжения источника на промежуток времени

необходимый для распространения волны от источника до данного сечения линии х.

Таким образом, напряжение падающей волны в любом сечении линии

Ипад = Um cos (а t - = Um COS (at - ax),

где и - - называется волновым числом.

Выражение, полученное для {/ ад. показывает, что в каждый данный момент t напряжение распределено вдоль линии по синусоиде (рис. 4-42). С течением времени это распределение перемещается от начала линии к нагрузке со скоростью v. Теория показывает, что для двухпроводных линий, расположенных в воздухе, скорость распространения волны 1

равна скорости света.

Расстояние, на которое волна переместится за время Т одного периода изменения напряжения источника, называется длиной волны:

За время Т источник возвращается к своему первоначальному фазовому состоянию. Поэтому длиной волны является расстояние между двумя точками волны с одинаковой фазой колебания, например расстояние между двумя гребнями (рис. 4-42).

Волновое число может быть выражено через длину волны:

со 2л

2л

В падающей волне напряжения, возникающей в линии без потерь, амплитуда колебаний не изменяется вдоль линии, а запаздывание колебаний по фазе

(р= ах

увеличивается пропорционально расстоянию х, пройденному волной. Волновое число а определяет изменение запаздывания колебаний по фазе на единицу длины.

Теория двухпроводной линии показывает, что в падающей волне отношение напряжения Unas, к току

активно, не зависит ни от частоты, ин от и равно:

координаты

пад 1/ 1 пад 1

пад

Эта величина называется волновым сопротивлением. Таким образом, ток падающей волны

и,п' I. х\ Um

- cos ш

cos (&t - ах).

Все указанные соотношения могут быть обнаружены и в отразкенной волне с той лишь разницей, что волна движется в противоположном направлении (в направлении - X), т. е. увеличение х вызывает не отставание, а опережение колебаний по фазе.

Бегущие и стоячие волиы в двухпроводной линии

Если отражения от нагрузки отсутствуют, то в линии возникнет лишь падающая волна. Этот режим линии называют режимом, бегущей волны. В бегущей волне амплитуда колебаний постоянна, а фаза колебания есть линейная функция расстояния, пройденного волной. Такой режим устанавливается в однородной бесконечно длинной линии, а также в линии конечной длины, в которой

отношение = Q соблюдается в любой точке линии,

в том числе и на ее конце. Последнее оказывается возможным лишь при активной нагрузке, равной волновому сопротивлению,

Z2 = Q.

Во всех остальных случаях нагрузка линии Zg Q представляет собой неоднородность, которая является причиной появления отраженной волны. При этом энергия, доставляемая линией к нагрузке, полностью не поглощается нагрузкой и остаток энергии возвращается обратно к генератору в виде отраженной волны.

При наличии отраженной волны распределение тока и напряжения вдоль линии существенно изменяется, так как оно является результатом интерференции (сложения) падающей и отраженной волн, в результате чего возникает стоячая волна.

Чтобы найти выражение для стоячей волны, будем считать, что нагрузка совсем не поглощает энергии и по-