этому амплитуды напряжений падающей и отраженной волн одинаковы:

{пад= Vm cos {at - ах); VoTp = lm COS (at + ax). Результирующее напряжение

О == С/пад loTp = fm [cos (caf - ax) -}- cos ((ot a;c)] = 21/ cos ax cos

Это выражение показывает, что в стоячей волне отсутствует линейная зависимость фазы от расстояния, а амплитуда волны

2Uff2 cos ах

зависит от координаты х, изменяясь .от наибольшего значения 2Um до нуля. Сечения линии, в которых наблюдаются наибольшие изменения амплитуды, называются пучностями, а сечения с наименьшими изменениями амплитуды - узлами. Местоположение узлов и пучностей не зависит от времени, т. е. и узлы и пучности неподвижны. В любых других сечениях линии напряжение изменяется во времени по синусоидальному закону, причем амплитуда колебания зависит от положения сечения.

Следовательно, если геометрическим образом бегущей (падающей) волны была синусоида, двшкущаяся вдоль линий со скоростью V, то геометрическим образом стоячей

Рис. 4-43. Изменение напряжения в стоячей волне.

волны является неподвижная синусоида, пульсирующая с частотой ш (рис. 4-43). Расстояние между соседними пучностями, так же как и между соседними узлами, X

равно -.

К аналогичным выводам можно было бы прийти в отношении стоячей волны тока. При этом можно было бы заметить, что при возникновении в линии режима стоячей волны точкам с пучностями напряжения соответствуют точки узловых значений тока, и наоборот. Это означает, что сопротивление линии, т. е. отношение напряжения к току в определенных сечениях линии, не является постоянной величиной, как в случае режима бегущей волны, а меняется от точки к точке. В точках с пучностями напряжения и узлами тока сопротивление бесконечно велико, -а в точках с пучностями тока и узлами напряжения оно равно нулю.

Иначе говоря, если входное сопротивление линии Zi в режиме бегущ,ей волны всегда равно волновому сопротивлению линии, то в режиме стоячей волны оно определяется длиной линии и нагрузкой на конце линии (рис. 4-44).

В общем случае, когда линия нагружена на произвольное сопротивление, от конца линии отразкается не вся Энергия, а лишь часть ее. При этом в линии возникает смешанный режим, характеризующийся наложением чисто стоячей волиы на чисто бегущую волну.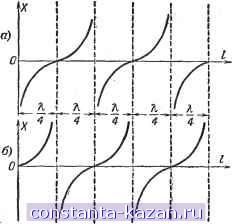

Рис. 4-44. Зависимость входного сопротивления от длины разомкнутой (а) и короткозамкн-утоЛ на конце (6) линии.

В результате напряжение и ток ни в одном сечении линии не обращаются в нуль, но существуют точки с минимальными и максимальными амплитудами.тока и напряжения, причем по-прежнему в точке максимального напряжения ток минимален, и наоборот. Расстояние между сечениями с максимальной (или минимальной) амплитудой по-прежнему равно Y Сопротивление ни в одном сечении линии

не обращается в нуль или бесконечность, но принимает очень большие значения в точках максимума напряжения и очень малые значения в точках максимума тока.

По отношению минимальной амплитуды напряжения (или тока) к максимальной судят о степени поглощения энергии нагрузкой. Это отношение называют коэффициентом бегущей волны. При нагрузке, равной волновому сопротивлению , т. е. при так называемо. ! согласованной нагрузке, этот коэффициент равеЧ единице. При непоглощаюшей нагрузке (короткое замыкание, разомкнутая нагрузка или чисто реактивная нагрузка) этот коэффициент равен нулю. Отсутствие согласования, т. е. наличие стоячих волн в линии, ведет к излишним затратам энергии. Поэтому на практике всегда стремятся устранить отражения полностью, а если это невозможнее то одни отраяйния стремятся скомпенсировать другими, чтобы в результате в линии осталась только чисто бегущая волна.

Линии с потерями

В реальных линиях всегда имеются потери электри- ческой энергии, связанные, например, с нагреванием проводников и диэлектриков, составляющих линию, с излучением и т. д. Если эти потери не слишком велики, то все вышесказанное о скорости распространения, длчне воля j и волновом сопротивлении остается прнблнж1м11о сира-

ведливым. Существенным отличием линии с потерями является уменьшение амплитуды тока и напряжения при движении волны вдоль линии из-зд потребления энергии волны в самой линии. Это уменьшение амплитуды с расстоянием X обычно называют затуханием и учитывают множителем ё~, где Р - коэффициент затухания линии, показывающий степень изменения амплитуды колебаний на каждую единицу длины линии. В результате для реальной линии выражение для бегущей волны напряжения принимает вид:

и = t/ e-P cos {at - ах).

, Коэффициент затухания линии выразкают в неперах на метр согласно определению;

г г

Р= 1п

где и mi и - амплитуды в сечениях линии л; и x-f- I. Этот же коэффициент можно выразить в децибелах на метр, если учесть, что 1 неп = 8,68 дб.

Коэффициент затухания линии прямо пропорционален погонному активному сопротивлению линии и обратно пропорционален ее волновому сопротивлению;

Р=2е= 2 у г-

Особенности распространения волн внутри прямоугольных волноводов

Волноводами называются металлические трубы, предназначенные для передачи радиоволн. Они применяются для соединения передатчика или приемника с антенной или для других высокочастотных соединений на волнах короче 2-3 дм.

На этих волнах двухпроводная линия применяться не может, так как при большом (по сравнению с длиной волны) расстоянии между проводами возникают потери, связанные с излучением электромагнитных волн в окружающее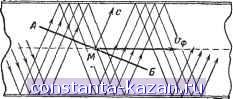

Рис. 4-45. Движение волн путем отражения от стенок волновода.

пространство, а уменьшение расстояния между проводами грозит опасностью пробоя при передаче по линии большой мощности. В волноводе электромагнитное поле заключено внутри металлической трубы, и поэтому потери на излучение отсутствуют. В отличие от коаксиального фидера, внутренний провод и поддерживающие его детали из диэлектрика в волноводе отсутствуют. Поэтому волновод характеризуется меньшей опасностью пробоя, а также меньшими потерями в металлических стенках и диэлектрике.

Электромагнитные волны распространяются в волноводе в результате последовательных отражений от его стенок (рис. 4-45). Интерференция многочисленных волн, отраженных от стенок, приводит к достаточно сложной структуре результирующего поля в волноводе. Однако

ясно, что для передачи энергии электромагнитных волн вдоль полновода в направлении его оси должна, устанавливаться бегущая волна, а в поперечных направлениях - стоячие волны с узлами и пучностями напряженности поля.

Не всякие типы электромагнитных волн могут проходить через волноводы. Представим себе, например, наиболее простую и широко распространенную поперечную электромагнитную волну, обозначаемую символом ТЕМ. В этой волне силовые линии

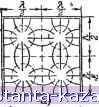Рис. 4-46. Волна ТЕ , в поперечном (с) и продольном (б) сечениях прямоугольного волновода.

Рис. 4-47. Волна ТМ в поперечном (с) й продольном (б) сечениях прямоугольного волновода.

напряженности электрического и магнитного полей полностью лежат в плоскости, перпендикулярной к направлению распространения волны, т. е. электрическое и маг-нитноегполя не имеют продольной составляющей. Такую структуру имеет поле на большом расстоянии от антенны, а также поле двухпроводной линии. В волноводе поперечная электромагнитная волна ТЕМ распространяться не может, так как электрические и магнитные силовые линии не могут одновременно находиться в плоскости поперечного сечения волновода и охватывать друг друга. Поэтому в волноводе возможно возбуждение лишь таких типов волн, в которых одно из полей - электрическое или магнитное - имеет продольную составляющую.

Волны, возбуждаемые в волноводе, могут быть объединены в две большие группы:

1) Поперечно-электрические волны, у которых вектор Е расположен только в поперечной плоскости волновода, а вектор Е наряду с поперечной составляющей имеет и продольную составляющую. Эти волны называются ТЕ- волнами (или Н- в о л н а м и),

2) Поперечно -магнитные волны, у которых вектор Н расположен только в поперечной плоскости, а вектор Е, кроме поперечной, имеет еще и продольную составляющую. Эти волны называются ТН-ъ о л-н а м и (или Е-в о л н а м и).

Представление о структуре поля этих типов волн в прямоугольном волноводе дают рис. 4-46 и 4-47, на которых отловые линии электрического поля изображены сплошными линиями, а магнитного поля -т- пунктиром. В поперечном сечении волновода поле состоит из отдельных

типичных для данной группы волн ячеек размером

Один тип волны отличается от другого по числу

ячеек стоячей волны, укладывающихся вдоль широкой и узкой стенки волновода. Эти два числа указываются в названии типа волн в виде индексов (ТЕш ТНп), которые определяют число полуволн, укладывающихся вдоль широкой (т) и узкой (п) стенок волновода.

Возникновение в волноводе того или иного типа волны зависит От формы и размеров поперечного сечения волновода, рабочей длины волны и способа возбуждения волн в волноводе. При этом возникновение сложных (высших) типов волн (с большим количе-1 лгЯТГШТШТПТп . ством ячеек) крайне нежела-

тельно, так как эти волны отличаются большими потерями энергии в стенках волновода и требуют значительных размеров волновода по сравнению с длиной волны.

Самую простую структуру поля в прямоугольном волноводе имеет волна ТЕд (рис. 4-48). Этот низший тип волны считают основным и используют в подавляющем большинстве случаев. Все остальные типы волн называют высшими.

В волне TEig электрические силовые линии лежат в плоскости поперечного сечения волновода и параллельны узкой его стенке. Вдоль широкой стенки укладывается одна полуволна, причем непряженность электрического поля около узких стенок равна нулю, а посредине максимальна. Магнитные силовые линии лежат в= продольных плоскостях, параллельных широкой стенки волновода. Напряженность магнитного поля имеет как поперечную, так и продольную составляющие. Поперечная составляющая магнитного поля меняется так же, как и напряженность электрического поля (т. е. равна нулю около узких стенок и максимальна посредине), а продольная составляющая, наоборот, имеет максимальное значение около узких стенок и равна нулю посредине. Вдоль узких стенок ни магнитное, ни электрическое поля не меняются. Вдоль оси волновода существует распределение, соответствующее бегущей волне. Это означает, что картина силовых линий на рис. 4-48,6 (а также 4-46, б и 4-47,6) изобразкена для какого-то момента времени. В следующий момент времени эта картина переместится вдоль оси волновода; за половину периода она переместится на расстояние, равное половине длины волны в волноводе, и т. д.

Длина волиы в волноводе не равна, а всегда больше длины волны в свободном пространстве. Это объясняется тт, что электромагнитные волны распространяются внутри волновода в результате последовательного отражения от его стенок. Выделим поверхность равных фаз (фазовый фронт) волны, движущейся под некоторым углом . к стенке волновода (на рис. 4-45 след этой поверхности обозначен отрезком АБ). Если скорость движения этой волны равна скорости света, то скорость перемещения одного и того же фазового состояния вдоль оси волновода (точка МУ больше, чем скорость света. Поэтому результирующая фазовая скорость pacпpotтpaнeния

Рнс. 4-48. Волна r£j в поперечном (а) н продольном (6) сечениях прямоугольного волновода.

радиоволн в волноводе больше скорости света. Например, для волны ТЕд

с

где а - размер широкой стенки волновода;

с = 3 -108 м/сек - скорость света.

Соответственно этому длина волны в волноводе больше, чем длина волны X в свободном пространстве,

Важной особенностью волноводов является то, что длина распространяющейся волны А не может быть больше некоторой критической длины' волны Акр, так как при А > Акр создаются такие условия отражения волн внутри волновода, при которых они колеблются между боковыми стенками, но не двигаются вдоль оси волновода.

Для волны TEig в прямоугольном волноводе

Для работы на основном типе волны рабочая волна должна быть меньше критической волны основного типа, но больше критической длины волны ближайшего высшего типа. Это определяет выбор размеров поперечного сечения волновода. Например, для прямоугольного волновода

<т- .....

Обычно размер широкой стенки волновода выбирают примерно 0,7Х. Размер узкой стенки определяет пробивную прочность и потери в стенках волновода. Обычно его выбирают равным (0,4-0,5) о.

Объемные резонато ры

Уменьшение емкости и индуктивности элементов колебательного контура с целью увеличения его резонансной частоты ограничено конструктивными возможностями. В дециметровом и сантиметровом диапазонах радиоволн создание колебательных контуров с сосредоточенными емкостью и индуктивностью становится практически невозможным, вместо них применяются колебательные контуры с распределенными параметрами, которые называются объемными резонаторами. В качестве объемных резонаторов используются, например отрезки прямоугольных или круглых волноводов, имею- щие длину, равную целому числу полуволн в волноводе и замкнутые с обоих концов металлическими стенками (рис. 4-49 и 4-50). Применяются н иные формы резонаторов.

Типы волн, возбуждаемые в объемных резонаторах, обозначаются так же, как в случае волноводов, но добавляется третий индекс р (ТЕщпр или Нтпр) указывающий количество полуволн поля, укладывающихся по длине резонатора В прямоугольных объемных резонаторах наиболее часто используют волну типа ТЕд^.

Для характеристики объемного резонатора обычно используют значения резонансной частоты fg (или Хд) и добротности Q.

1792