Чаще всего электрический ток возникает за счет упорядоченного движения наиболее легких и подвижных отрицательных частиц - электронов. Однако в электротехнике за положительное направление электрического тока условно приняли направление движения положительных зарядов под действием разности потенциалов, т. е. направление от большего потенциала V] к меньшему потенциалу Vg.

Закон Ома

Электрический ток в проводниках возникает лишь в тех случаях, если в них имеются области, находящиеся lipH разных потенциалах. Закон Ома, подтвер'ждаемый многочисленными экспериментами, показывает, что ток /

Рис. 3-8. Условное изображение протекания тока по участку проводника с сопро-, тиБлением R.

прямо пропорционален разности потенциалов V] - V2 на концах участка проводника (рис. 3-8) и обратно пропорционален сопротивлению R этого участка:

~ R

здесь R - величина сопротивления участка проводника, характеризующая противодействие этого участка электрическому току.

Сопротивление

Разность потенциалов на концах проводника часто называют напряжением:

£/ = - Vg.

В таком случае сопротивление равно отношению напряжения на концах проводника к току, проходящему через него.

Практической единицей сопротивления является о м {ом) - сопротивление проводника, в котором возникает ток в один ампер при напряжении в один вольт.

Сопротивление зависит от геометрических размеров проводника, его материала и температуры. У протяженных проводников постоянного сечения сопротивление пропорционально длине / проводника и обратно пропорционально его поперечному сечению S:

где Q - величина, зависящая лишь от материала проводника и называемая удельным сопротивлением материала.

При пользовании этой формулой R выражают в омах, / - в сантиметрах, а S - в квадратных сантиметрах. Таким образом, удельное сопротивление q должно выражаться в ом о-с антиметрах (ом-см). Эта единица равна удельному сопротивлению такого материала, куб с ребром в 1 см которого- имеет сопротивление 1 ом, если ток протекает от одной грани к противоположной.

Величина, обратная сопротивлению,

характеризует проводящие свойства проводника и называется проводимостью. Проводимость измеряется в единицах, называемых обратными омами

(- , или мо\. ом J

Величина, обратная удельному сопротивлению, 1

о = - Q

называется удельной (объемной) проводимостью или электропроводность ю. Она

измеряется в -?- .

Соединение сопротивлений

Участки проводников с различными сопротивлениями могут соединяться друг с другом, образуя последовательное (рис. 3-9), параллельное (рис. 3-10) и смешанное (рис. 3-11) соединения.

Рис. 3-9. Последовательное соеД1Гнение сопротивлений.

При последовательном соединении эквивалентное (общее) сопротивление цепи R равно сумме сопротивлений, составляющих цепь

Нг + /?2+ i?3+ .. . +Rn-

Если цепь состоит из п последовательно соединенных одинаковых сопротивлений то

R = nR.

г

1-Х I

Рис. 3-10. Параллельное соединение сопротивлений.

Рис. 3-11. Смешанное соединение сопротивлений.

При параллельном соединении эквивалентное сопротивление цепи R меньше любого из сопротивлений, составляющих цепь, и может быть определено по формуле

-L = JL + L

+ -4- + -.- +

(т. е. в данной случае складываются не сопротивления, а проводимости).

Если цепь состоит из п параллельно соединенных одинаковых сопротивлений R, то

При. смешанном соединении эквивалентное сопротивление определяется путем объединения последовательных участков и параллельных ветвей.

Пример. Если на рис. 3-П ;?i = 2 000 ом; Ri = 1 ООО ол и ;?з = 3 ООО ом. то

3 , 1

2 3

R+Ri

Замкнутая цепь постоянного тока

Цепь постоянного тока (рис. 3-12) состоит из в и е ш-н е г о сопротивления /?иисточника тока, который поддерживает постоянную разность потенциалов на внешнем сопротивлении и имеет собственное внутреннее сопротивление Rq.

Ток / должен быть замкнут, так как он представляет собой движение зарядов, которые нигде не накапливаются.

Во внешней цепи ток течет от большего (Vj) потенциала к меньшему (Ка) и согласно закону Ома

Vi - Vi= IR.

Рис. 3-12. Замкнутая цепь постоянного тока.

Но эта разность потенциалов Vi - Vs не может быть причиной движения тока по внутреннему сопротивлению, так как < Vi. Следовательно, в источнике тока должна создаваться разность потенциалов

V;-vl=-IR,.

обусловливающая движение тока на участке Rq. Суммируя эти равенства, получим:

[V - V2} + {Vj - Vl) = /(R Ro).

Основной задачей источника тока является создание скачков потенциала

AVj = Vj - V[;

обеспечивающих движение тока по замкнутой цепи. Сумма скачков потенциала

£ = AFi -f AF2

называется электродвижущейсилой(э. д. с.) источника. Эта величина является основной характеристикой источника и измеряется в вольтах (е).

Вводя э. д. с. источника в суммарное равенство, получаем закон Ома для замкнутой цепи:

п

.Отсюда, в частности, следует: Vi - = £ -

т. е. разность потенциалов на зажимах источника зависит' от тока; она равна э. д. с. источника минус падение напряжения на внутреннем сопротивлении источника.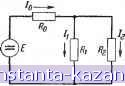

Рис. 3-13. Пример разветвленной цепи постоянного тока.

Разветвленная цепь постоянного тока

Разветвленной цепью постоянного тока называется такое соединение источников тока и сопротивлений, при котором для тока имеются два или более путей. Каждый из этих путей является замкнутым контуром. Всякая точка разветвленной цепи, в которой сходятся не менее трех проводников, называется узлом. Например, электрическая цепь, изображенная на рис. 3-13, содержит три замкнутых контура и два узла. .

Величины токов во всех сопротивлениях разомкнутой цепи могут быть определены, если известны величины э. д. с. и сопротивлений R, составляющих электрическую цепь. Расчет токов может быть сделан при помощи уравнений Кирхгофа.

Уравнения Кирхгофа

Первая система уравнений Кирхгофа относится к узлам электрической цепи. Токи, направленные к узлу, будем считать положительными, а токи, исходящие из узла, - отрицательными. Поскольку заряд в узле накапливаться не может, алгебраическая сумма сил токов, сходящихся в узле, равна нулю:

2

Вторая система уравнений Кирхгофа относится к замкнутым контурам, которые можно выделить в разветвленной цепи. Применяя закон Ома к этим контурам, можно заметить, что в любом произвольно выбранном замкнутом контуре сумма э. д. с. равна сумме произведений токов на сопротивления соответствующих участков контура (т. е. сумме падений напряжений на сопротивлениях контура, включая и внутренние сопротивления источников тока):

m п

/ I £к = 2 kRk-к=1 k=l

При составлении уравнений Кирхгофа нужно следить за тем, чтобы число уравнений равнялось числу искомых величин и чтобы одни уравнения не являлись следствием других.

Например, .для определения трех различных токов в электрической цепи, изображенной на рис. 3-13, можно составить первое уравнение Кирхгофа:

и два вторых уравнения Кирхгофа:

foRo + fiRi = Е\ ,

hRi - 1%R = 0. Совместное решение этих уравнений дает:

R0R1 ~Г R0R2 12

R0R1 + R0R2 + R1R2

RoRi + 02 Ь 12

Использование уравнений Кирхгофа для расчета сложных электрических цепей связано с трудоемкими преобразованиями. Количество вычислений может быть резко со-сокращено применением изложенных ниже принципов в методов расчета.

Принцип наложения

При наличии в электрической цепи нескольких э. д. с. принцип наложения (суперпозиции) позволяет вычислять значения токов в любом участке цепи как алгебраическую сумму токов, создаваемых на этом участке каждой э. д. с. в отдельности.

контурам, являются алгебраической суммой соответствующих,контурных токов.

Контурные токи могут быть найдены с помощью вторых уравнений Кирхгофа, число которых равно числу соприкасающихся контуров (т е. меньше, чем в предыдущем случае).

На схеме, выбранной в ка- /?g

честве примера (рис. 3-15), имеются два соприкасающихся контура. Считая направление контурного тока, текущего по часовой стрелке, за положительное, составим два уравнения Кирхгофа для определения контурных токов: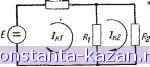

Рис. 3-15. Применение метода контурных токов.

Рис. 3-14. Применение принципа наложения к цепи с двумя источниками тока.

Пусть, например, мы интересуемся током в цепи, содержащей два источника тока с э. д. с. Е' и Е (рис. 3-14, о).

При действии в цепи лишь э. д. с. Е' (рис. 3-14, б) согласно предыдущему примеру получим:

г' Е 1 Ч~ 2

При действии в цепи лишь э. д. с. £ (рис. 3-14, е) получим:

RqRi ~\~ RqRz ~г R1R2

При действии в цепи обеих э. д. с. (рис. 3-14, а) согласно принципу наложения получим:

F{Ri + R2)-E Ri

RoRi + RoR2 + RiR

h = lo + l o

Следствием принципа наложения является пропорциональность меаду э. д. с, действующей в цепи, и током, порождаемым этой э. д. с. Такая пропорциональность имеет место только в линейной цепи. Таким образом, линейной электрической цепью называется такая цепь, для которой справедлив принцип наложения.

Метод контурных токов

Разветвленную цепь можно рассматривать как совокупность соприкасающихся друг с другом замкнутых контуров. Каждому контуру можно приписать некоторый контурный ток 1. При этом действительные токи в участках, принадлежащих нескольким

RJkt. + Ri (/к1 - /к£) = Е; RifK2 + Ri (/к2 - /ki) = 0.

Решая эти уравнения относительно контурных токов, получим:

/к, = £

R1 + R2

/кй = Е

RoRi Ь 02 Ь RiR Ri

RoRi 02 + RiRz

Однако интерес представляют не контурные токи, а действительные токи, протекающие по проводникам цепи. Поэтому, возвращаясь к обозначениям рис. 3-13, находим:

R1 + R2

2 - 1к9. = Е

RoRi + 02 -г R1R2 R2

RoRi + 02 + 12 Ri

RqRi Ь 02 ~г RiR

Метод узлового напряжения

Если электрическая цепь содержит лишь два узла (при любом количестве п ветвей между узлами), то удобным методом определения токов в ветвях цепи является метод узлового напряжения.

Электродвижущая сила Ек в любой из ветвей такой цепи расходуется на создание падения напряжения на

сопротивлении ветви R = -уг- и на поддержание напря-

к

жения t/j.a между двумя узлами цепи (у з л о в.о г о напряжения):

£к= t/l.2+ /к/?К-

Разделив это выражение на R, получим: EkGk = Uj.Gk + Ik-

Суммируя подобные равенства для всех п ветвей, получим:

2 £кСк=1/г.2 S 2 к-

k=i k=l k=l