где а - угол между вектором В и нормалью п к площадке S; Во - проекция вектора В на нормаль п к площадке S.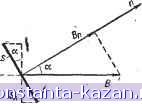

Рис. 3-21. К определению потока магнвдиой индукции через пло- . щадку S.

3-4. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ

Явление электромагнитной индукции

При движении проводника в магнитном поле в проводнике возникает электродвижущая сила индукции, а если при этом контур проводника замкнут, то в нем появляется электрический ток индукции. Это явление электромагнитной индукции возникает всегда при пересечении движущимся проводником магнитных силовых линий, а также при любом изменении потока магнитной индукции через контур проводника. Электродвижущая сила индукции пропорциональна скорости изменения числа линий магнитной индукции, охватываемых контуром проводника, т. е. пропорциональна скорости изменения потока магнитной индукции через контур проводника:

где ДФ - изменение потока за достаточно малый промежуток времени А t.

Таким образом, для электромагнитной индукции необходимо пересечение проводником линий магнитной индукции; при движении проводника вдоль линий магнитной индукции э. д. с. индукции равна нулю.

Направление индукционного тока может быть определено по следующему правилу: индукционный ток имеет такое направление, при котором он создает через площадь, ограниченную контуром, собственный поток магнитной индукции, стремящийся компенсировать то изменение потока магнитной индукции, которое его вызывает.

Единица измерения потока магнитной индукции

Если замкнутый проводник, в котором возникла э. д. с. индукции Е, имеет сопротивление R, то

ДФ At

AO=.lAtR qR.

На этом основании за практическую единицу потока магнитной индукции принимают такой поток через контур проводника, при убывании которого до нуля через поперечное сечение проводника, имеющего сопротивление 1 ом, протекает количество электричества, равное 1 к. Эта единица носит название в е б е р (еб).

Практическая единица магнитной индукции есть веберна квадратный метр (вб/м^).

Самоиндукция

Электромагнитная индукция вызывается изменением потока магнитной индукции через контур проводника. При этом совершенно безразлично, чем обусловлено это изменение. Оно, например, может быть вызвано непостоянством тока, текущего через проводник. Если по проводу течет непостоянный ток, то магнитное поЛе этого тока также непостоянно. Следовательно, меняется поток магнитной индукции через контур проводника, что ведет к возникновению в контуре э. д. с. индукции. Таким образом, изменение тока в контуре является причиной возникновения э. д. с. индукции в этом же самом контуре. Это явление называется явлением самоиндукц ИИ.

Проводники различной формы обладают различной способностью обнаруживать явление самоиндукции. Наиболее интенсивно это явление протекает в катушках индуктивности, которые представляют собой провод, согнутый в виде витков. Способность контура к самоиндукции характеризуется коэффициентом самоиндукции, который может быть введен следующим образом.

Согласно закону Био - Савара ток, протекающий по витку проводника,- создает магнитное поле, напряженность и индукция которого пропорциональны току /. Следовательно, поток магнитной индукции Ф, пронизывающий виток, пропорционален току, текущему по витку,

Коэффициент пропорциональности L между током в проводнике и величиной магнитного потока, созданного этим током, называется коэффициентом самоиндукции.

Чем больше коэффициент самоиндукции, тем больше величина э. д. с. самоиндукции:

ДФ , Д/

Величина коэффициента самоиндукции определяется геометрической формой и размерами проводника.

Практическая единица коэффициента самоиндукции называется генри (гн); она равна коэффициенту самоиндукции такого контура, который пронизывается потоком магнитной индукции в 1 еб при токе в ием 1 а.

Взаимная индукция

Взаимной индукцией называется возникновение э. д. с. в одном проводнике вследствие изменения величины тока в другом проводнике или вследствие изменения взаимного расположения -проводников. Это явление объясняется тем, что при изменении тока в одном из проводников или при изменении их взаимного расположения происходит изменение потока магнитной индукции, созданного током первого проводника и проходящего через контур второго проводника, что вызывает возникновение э. д. с. индукции во втором проводнике.

Обозначим через Ф] весь поток магнитной индукции, создаваемый током контура 1, а через Ф^.г часть этого потока, пронизывающую контур 2 (рис. 3-22, а). Поток Ф1.2 создан током /j и поэтому пропорционален этому току:

Ф1.2=Л?1.2/1-

Коэффициент пропорциональности Ж^.г называется коэффициентом взаимоиндукции; он численно равен потоку магнитной индукции, который создается током в 1 о одного из контуров и пронизывает другой контур.

Изменение тока /j приводит к изменению потока Ф1.2 и появлению э. д. с. взаимоиндукции во втором контуре величиной

Если за основной контур, создающий магнитное поле, считать контур 2 (рис. 3-22, б), то контур 1 пронизывается потоком

Ф2.1=М2.1/2.

изменение которого вызывает появление в контуре / э. д. с. взаимоиндукции

At

а) -2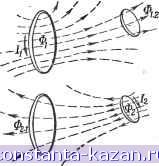

Рис. 3-22. К опредсчению коэффициента взаимоиндукции.

В теоретической электротехнике доказывается, что

/12.1 = Л?1.2 = /W.

Величина коэффициента взаимной индукции М двух контуров определяется геометрической формой, размерами и относительным положением этих контуров.

Единица измерения коэффициента взаимоиндукции а1галогична единице измерения коэффициента самоиндукции.

3-5. ПЕРЕМЕННЫЙ ТОК

Синусоидальная электродвижущая сила

Если в электрической цепи действует изменяющаяся по величине э. д. с, то она вызывает в цепи перемен-н ы й т о к. Наибольшее распространение в технике получили э. д. с. и токи, синусоидально (гармонически) изменяющиеся во времени Одним из способов получения синусоидальной э. д. с. является равномерное вращение плоского проводящего витка в однородном магнитном поле (рис. 3-23). Поток магнитной индукции, пронизывающий виток, в этом случае меняется синусоидально. Следовательно, синусоидально будет меняться и э. д. с. индукции (рис. 3-24, б):

Е= Вт cos (at.

В этом выражении Е; обозначает амплитуду э. д. с, т. е. наибольшее ее значение (размах колебаний). Греческой .буквой ю обозначена угловая скорость вращения витка в магнитном поле, которая связана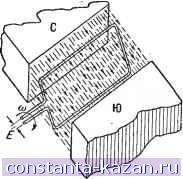

Рис. 3-23. Получение синусоида.чьной э. д. с.

С частотой / и периодом Т вращения витка зависимостью

2п

ю = 2я/ =

т

Ясно, что период вращения витка и период (полный цикл) изменения синусоидальной э. д. с. индукции - оди-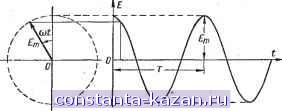

Рис. 3-24. Графическое изображение синусоидальной э. д. с.

наковы. Период измеряется в секундах (сек), угловая частота в радианах в секунду (рад/сек), а частота в периодах в секунду или герцах (1 гц = 1 пер/сек).

Цепь переменного тока

Синусоидальная э. д. с. Е может быть приложена к цепи переменного тока включающей в себя сопротивле-

Рис. 3-25. Цепь переменного тока.

ния i?, катушки индуктивности L и конденсаторы С (рис. 3-25). Под действием синусоидальной э. д. с. в пени протекает синусоидальный ток.

Может, однако, возникнуть сомнение в возможности протекания тока по цепи, содержащей конденсатор. Ведь материальными носителями электрического тока являются свободные заряды (электроны). Легко перемещаясь под

действием э. д. с. по сопротивлениям, катушкам индуктивности и монтажным проводам, электроны, естественно, не могут преодолеть разрыва в электрической цепи, которым является промежуток между обкладками конденсатора, заполненный диэлектриком. Постоянный ток не может протекать через конденсатор.

Но переменный ток может течь через конденсатор. Заметим, что даже при подключении конденсатора к источнику постоянной э. д. с. в цепи протекает ток, хотя и не все время. Он течет лишь до тех пор, пока конденсатор не зарядится, т. е. пока на обкладках конденсатора не возникнет разность потенциалов, компенсирующая э. д. с. источника. При этом через диэлектрик между обкладками конденсатора заряды, естественно, не двигаются; протекание тока заключается в доставке зарядов от источника к обкладкам конденсатора (и от обкладок к источнику).

Аналогичной является картина протекания тока в случае подключения конденсатора к источнику синусоидальной э. д. с. При этом обкладки конденсатора непрерывно перезаряжаются и по цепи двигаются заряды, необходимые для этой перезарядки.

Метод комплексных амплитуд (символический метод)

Для упрощения записей и преобразований в теории переменных токов часто используют комплексные числа. Рис. 3-24, а показывает, что синусоидальная э. д. с. может быть изображена в виде вектора длиной Е^, вращающегося против часовой стрелки с угловой скоростью (о (рад/сек). При этом угол между вектором и вертикальной осью равен (0, а проекции вектора на вертикальную ось

Ет cos Ш

соответствуют мгновенным значениям синусоидальной э. д. с.

Это позволяет принять вертикальную ось за действительную ось комплексной плоскости, а горизонтальную ось - за мнимую ось и представить вектор синусоидальной э. д. с. в виде комплексного числа

Ё = ErJ = Em (cos + / sin wO,

где j = У - 1 называется мнимой единицей.

Модуль этого комплексного числа £ = Е^ определяет амплитуду колебания э. д. с, а аргумент (О/ - фазу колебания, которая измеряется в радианах, градусах или долях периода колебаний и определяет состояние колебательного процесса в данный момент времени.

Ток /, протекающий по цепи под действием э. д. с. Ё, также может быть представлен комплексным числом

с аргументом, отличающимся на угол ф, поскольку в общем случае э. д. с. и ток в цепи переменного тока могут изменяться не синфазно, а быть сдвинутыми по фазе на угол р.

Если в комплексах Ё и / опустить множитель ё'*, то они называются комплексными амплитудами. Точка над буквой ставится для того, чтобы отличить комплексные амплитуды от обычных амплитудных значений.

Переход от комплексных амплитуд к мгновенным значениям, как это следует из предыдущего, сводится к добавлению множителя е'* и к определению действительной части полученного комплекса:

£ = ReE.

Элементы цепи переменного тока

Амплитуда тока в цепи переменного тока определяется величинами R, L и С. Таким образом, эти три элемента цепи играют роль сопротивлений, но между ними имеются существенные различия.

Во-первых, сопротивление R поглощает электрическую энергию, доставляемую в цепь источником питания, а катушка индуктивности и конденсатор энергии не поглощают; они лишь накапливают эту энергию в течение одной половины периода (в виде энергии магнитного поля катушки или энергии электрического поля конденсатора) и возвращают ее обратно источнику питания в течение другой половины периода. Чтобы подчеркнуть это различие сопротивление R называют активным сопротивлением, а сопротивления катушки индуктивности и конденсатора называют реактивными (безваттными) сопротивлениями.

Во-вторых, активное, индуктивное и емкостное сопротивления по-разному зависят от частоты w приложенной к цепи э. д. с. Активное сопротивление-слабо зависит от частоты- лишь на очень высоких частотах приходится считаться с зависимостью активного сопротивления от частоты. Величина индуктивного сопротивления прямо пропорциональна частоте:

Xl = £,

а величина емкостного сопротивления обратно пропорциональна частоте:

В-третьих, напряжение и ток в активном и реактивных сопротивлен'иях находятся в различных фазовых соотношениях. Ток /, протекающий по активному сэпротивлению (рис. 3-25), создает падение напряжения l/i, совпадающее по фазе с током. Но в реактивных сопротивлениях фазы тока и напряжения отличаются на 90°, причем в индуктивном сопротивлении ток / отстает по фазе от напрял ния й^на 90°, а в емкостном сопротивлении ток / опережает по фазе напряжение Ос на 90°.

Математически это обстоятельство находит отражение в том, что отношение напряжения к току в случае активного сопротивления является действительным числом:

а в случае реактивного сопротивления - мнимым числом: Ul

Физической причиной мнимости реактивных сопротивлений является отсутствие поглощения энергии в этих сопротивлениях.

Закон Ома для цепи переменного тока

В цепи переменного тока, изображенной на рис. 3-25 значение э. д. с. в любой момент времени должно быть равно сумме мгновенных падений напряжения на сопротивлениях цепи. Это значит, что комплексная амплитуда э. д. с. равна сумме комплексных амплитуд напряжени15 на сопротивлениях цепи:

Ё = Он +0l + Uc-