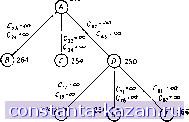Рис. 10.26. Поиск с деревом решений из примера 7.2 с улучшенной границей для задачи о назначениях.

циклом) уже не будет необходимым, так как его нижняя граница, а именно 254, больше чем 251. Прежняя граница для С, равная 248 (меньше 251), была недостаточной для того, чтобы прекратить ветвление в этом узле. Таким образом, улучшенная граница позволяет сэкономить два узла в дереве решений поиска, как это показано на рис. 10.26. Это дает экономию только на 2/9 для этой маленькой задачи, но для задач большого размера получается большой процент экономии узлов дерева, т. е. числа задач о (п. на п) назначениях, которые следует решить

8. Задачи

1. Показать, что если неориентированный граф G удовлетворяет условиям: (1) для каждого положительного целого числа к <С

<; у (п - 1), число вершин со степенью, не превосходящей к, меньше чем к, (2) если число вершин со степенью, не превосходящей у (п - 1), меньше или равно у (п - 1), то оно имеет гамиль-

но НОВОЙ границей для подзадачи С будет V [АР) + V {АР-) = = 248 + 6 = 254, вместо предыдущего значения 248. Новой границей для подзадачи D будет V [АРо) + V (АР-) = 250 + + О = 250 - ТО же, что и раньше. (Граница для В останется, конечно, неизменной, так как решение задачи В является на самом деле гамильтоновым циклом. Теперь ветвление нужно делать в узле D (так как 250 < 254), а не в С, как в предыдущем случае. Это ветвление приводит, как и прежде, к подзадачам G, Я и 7, и наилучшее решение (подзадача Я) имеет значение 251. Дальнейшее ветвление в С (где решение не является гамильтоновым

ТОНОВ ЦИКЛ (см. [25, 29]. Заметим также, что граф, состоящий из единственного гамильтонова цикла, не удовлетворяет вышеприведенным условиям, т. е. условия достаточны, но не являются необходимыми).

2. Доказать, что если в неориентированном графе G для любой пары несмежных вершин xi и xj степени удовлетворяют условию

d(Xi) + d{xj) > п,

то граф G имеет гамильтонов цикл (см. [26]).

3. Рассмотрим решетчатый граф G, образованный р горизонтальными и q вертикальными линиями, где каждая точка пересечения рассматривается как вершина и каждый отрезок между соседними точками пересечения решетки - как ребро. При каких р VI q граф G имеет гамильтонов цикл.

4. Показать, что граф, вершины и ребра которого соответствуют вершинам и ребрам /г-мерного гиперкуба, имеет гамильтонов цикл.

5. Показать, что в графе из задачи 4 гамильтонова цепь между двумя диаметрально противоположными вершинами существует тогда и только тогда, когда п нечетно.

6. Доказать, что в каждом полном антисимметрическом ориентированном графе существует гамильтонова цепь.

7. Используя методы разд. 2.1, 2.2 и 2.3, либо найти все гамильтоновы циклы в графе из рис. 10.27 (если такие циклы существуют), либо показать, что таких циклов нет. Сравнить вычислительную трудоемкость этих методов.

8. Р1спользуя метод разд. 2.3, проверить, что граф, изображенный на рис. 10.28, не содержит гамильтонова цикла. Доказать тот же результат другим способом.

9. Для задачи коммивояжера с приводимой ниже матрицей реберных весов С вычислить нижние границы оптимальных решений, используя задачи о назначениях и о кратчайшем остове.

10. Найти кратчайшую гамильтонову цепь между вершинами 4 и 7 для графа из задачи 9.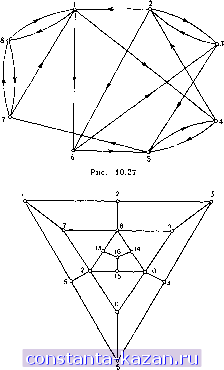

Рис. 10.28.

11. Найти абсолютно кратчайшую гамильтонову цепь в граф( из задачи 9.

12. Решить задачу коммивояжера с матрицей реберных aecoi из задачи 9, используя алгоритм поиска с деревом решений hi раздела 7.1 и правило ветвления В.

13. Решить задачу 1-2, используя тот же самый метод, но npi вычислении нижних границ, действуя в соответствии с результата ми разд. 7.4.