) Поток не будет конформальным, если, например, существует -\- р единичных потоков, использующих дугу в направлении от к ly, и р единичных потоков, использующих дугу в противоположном направлении, и все эти потоки, таким образом, дают общий поток от Xi к Xj, равный В общем случае два потока и будут конформалъными, если для любой дуги (а:;, Xj) будет I j.\pji = о,

Фу, . . ., Фк, li раз, то I можно записать в виде

l=Yhio(Pi)+ I о(ф,), i=i i=i

где суммирование понимается как сложение потоков в указанном выше смысле.

В процессе доказательства теоремы 2 получен другой важный результат, а именно что единичные потоки, на которые разложен поток I, являются конформалъными, т. е. если - значение потока на дуге (х;, Xj) графа G, то существует всего единичных потоков, которые все используют эту дугу в направлении от Xj к Xj 1).

Рис. 11.4 дает пример потока и его декомпозицию на простые цепи (от S к f) и циклы.

3. Простые варианты задачи о максимальном потоке (от sat)

Мы дадим теперь ряд задач, связанных с потоками, которые просто сводятся к аадаче о максимальном потоке (от s к t), рассмотренной выше.

3.1. Графы со многими источниками и стоками

Рассмотрим граф с щ источниками и стоками и предположим, что поток может идти от любого источника к любому стоку. Задачу нахождения максимального общего потока от всех источников ко всем стокам можно преобразовать в простую задачу о максимальном потоке (от S к t) путем добавления нового искусственного источника S и нового искусственного стока t с добавлением дуг, ведущих от S к каждому истинному источнику и от каждого истинного стока к t.

На рис. 11.5 показано, как множество источников и стоков может быть сведено к единственному источнику и единственному стоку. Пропускные способности дуг, ведущих от s к источникам, могут быть выбраны равными бесконечности или в случае, когда производительность источника Sh ограничена, пропускная способность соответствующей дуги (s, s) может быть выбрана равной этой границе. Точно так же пропускные способности дуг, ведущих

ют стоков к t, могут быть ограничены некоторой величиной (зависящей 01 стоков) или положены равными бесконечности, если такой границы нет.

Если в задаче некоторые стоки должны снабжаться только определенными источниками и наоборот, то она уже не будет

Граф 6

Стоки

Рис. 11.5.

простой разновидностью задачи о максимальном потоке (от s к. t) в становится задачей о многопродуктовом потоке. Эта задача упоминалась во введении (см. задачу (III)).

3.2. Графы с пропускными способностями дуг и вершин

Пусть в графе G дуги имеют пропускные способности q, в пусть, в дополнение к этому, вершины графа имеют пропускные способности Wj (/ = 1, 2, . . ., и), скажем, такие, что полный поток, входящий в вершину xj, должен иметь значение, меньшее, чем W}, т. е.

2 li; ? всех xi,

j6r-4 j)

Пусть требуется найти максимальный поток между вершинами s в t такого графа.

Определим граф так, чтобы каждая вершина Х} графа G соответствовала двум вершинам xjuxjB графе G , причем каждой дуге (xi, Xj) из G, инцидентной вершине xj, соответствует дуга (Xi, xf) из Go, инцидентная вершине Xj, и каждой дуге {xj, х^) из G, исходящей из Xj, соответствует дуга {xJ, xt) из Go, исходящая 03 xJ. Кроме того, введем дугу между xj ж xJ с пропускной способностью Wj, т. е. равной пропускной способности вершины Xj.

На рис. 11.6 (а) дан пример графа с пропускными способностями дуг и вершин, а на рис. 11.6 (б) показан граф Go, построенный в соответствии с приведенным описанием. Так как полный поток, входящий в вершину Xj, необходимо должен протекать по дуге (Xj, xj) с пропускной способностью Wj, то максимальный поток в графе G с пропускнь{ми способностями дуг и вершин равен максимальному потоку в графе Go, имеющем только пропускные способности дуг. Следует заметить, что если минимальный разрез

Xl У^г Х; ?2,4 4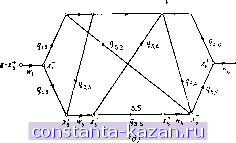

Рис. 11.6. (а) Граф, вершинам и дугам которого приписаны пропускные способностиа (б) Эквивалентный граф, в котором пропускЕше способности имеют только дуги,

в Go не содержит дуги вида (х/, xJ), то пропускные способности вершин в G пассивны и излишни. Если же минимальный разрез в Go содержит такие дуги, то соответствующие вершины в G насыщены подученным максимальным потоком.

ЗаЗ Графы, у которых пропускные способности дуг ограничены сверху и снизу

Рассмотрим граф G = (Х, А), дуги (xj, ху) которого имеют пропускные способности (верхние границы потока), скажем, q, а также имеют нижние границы потока, скажем, гц. Допустим,