что мы хотим узнать, существует ли допустимый поток между s и f, т. е. поток Ij;, удовлетворяющий для всех дуг (ij, Xj) из G условию (11.1) и, кроме того, неравенствам гц Чц-

Начнем с введения в графе G нового искусственного источника So и искусственного стока fa и построим новый граф Ga- Для каждой дуги {xi, xj), у которой Ф О, введем дуги (s , Xj) и (xj, fa) с пропускными способностями г^у И С нижней границей 0. Уменьншм qj до qa - Гц, а г^; до 0. Кроме того, введем дугу (f, s)

с = оо и Tts = 0.

Применяя, например, эти преобразования к графу, изображенному на рис. 11.7 (а) и имеющему только две дуги с ненулевыми нижними границами, ползучим граф, показанный на рис. 11.7 (б).

2 (0.92,4) j4 C46;?4.6) £в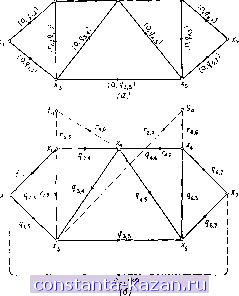

Рис. 11.7. (а) Граф с верхними и нижними границами потоков, проходящих по дугам, (б) Преобразованный граф, в котором для потоков имеются лишь верхние границы (даны значения верхних границ, все нижние границы равны нулю).

4. Максимальный поток между каждой парой вершин

В некоторых случаях, например когда граф представляет телефонную сеть, вершины которой соответствуют станциям, а дуги - телефонным линиям, может потребоваться найти максимальную скорость передачи сообщений между двумя любыми станциями s и f. При этом предполагается, что в любой фиксированный момент времени каждая станция может быть связана с произвольной другой, но лишь с одной станцией. В данном примере пропускная способность кабеля равна числу независимых разговоров,.

Найдем теперь максимальный поток между искусственными вершинами За и ta преобразованного графа Ga- Если значение максимального потока (от Sa к ta) ссть (т. 6. ссли всс дуги, выходящие

из Sa, и все дуги, входящие в ta, насыщены) и, скажем, поток по дуге (t, s) равен Its, то в первоначальном графе существует допустимый поток со значением Its- В этом можно убедиться так. Если мы вычитаем из потока в дугах (х^, ta) и (s, xj) и добавляем к потоку в дуге (х;, Xj), то значение полного потока от Sa к ta уменьшастся на величину rj, потоки по дугам (Х;, ta) и (Sa, Xj) уменьшаются до нуля, а поток по дуге (х;, Xj) принимает значение Itj, rtj qij ([конечное значение lij равно г;,

если первоначальное значение lij, соответствующее максимальному потоку, равно нулю и конечное значение lij равно qij, если первоначальное значение Itj является максимально возможным, т. е. qij - г;). Шаг, состоящий в вычитании потока из максимального потока, противоположен шагу увеличения в алгоритме максимального потока. Так как мы допустили, что максимальный поток от Sa к ta равен 2 ijf то процесс вычитания потока при-

rtjO

ведет в конечном итоге к нулевому потоку от Sa к ta (сделав тем самым эти две искусственные вершины и инцидентные им дуги излишними) и поток во всех дугах с г^ О будет лежать в пределах Tij lij qtj. Конечный результат является, следовательно, циркуляцией потока в графе, причем значение этого потока равно Its- С другой стороны, справедлива

Теорема 3. Если значение максимального потока {от Sa к ta) в графе Ga не равно 2 Ui * графе G не существует никакога

допустимого потока.

Доказательство этой теоремы предлагаем в качестве упражнения читателю (см. задачу 5).

которые могут вестись по нему. Подобная ситуация имеет место и в случае, когда граф представляет сеть дорог с односторонним движением и требуется определить, как односторопнее движение влияет на максимум транспортного потока между двумя районами, если эти районы рассматриваются обособленно друг от друга.

Как было отмечено во введении, эта задача может быть решена просто с помощью задачи о максимальном потоке (от s к f) для всех пар вершин (s, f). Однако такой метод излишне трудоемок, поэтому мы изложим здесь алгоритм Гомори и Ху [14], который в случае неориентированных графов намного более эффективен. Так как этот алгоритм использует два важных понятия, то мы сначала обсудим их, чтобы сделать более ясным описание самого алгоритма.

4.1. Потоковая эквивалентность

Теорема 4. Пусть fu - значение максимального потока от вершины Xi к вершине Х] графа G. {Так как G - неоршнтированный граф, то fi] = fji). Эти потоки удовлетворяют состношению

fij>min[fih, fkj] для всех г, f, к. (11.8)

Доказательство, Если {Х^, Х„) - минимальный разрез, даюгпчй fij, т. е.

fi} - v{Xo, Хо), XiXo, ijXo,

то при Хи € выполняется неравенство ftj fj, так как {Х^, Хд) является также разрезом, отделяющим х^ от xj, а при 6 Хд справедливо неравенство ftj fi, так как (Zq, Xq) является также разрезом, отделяющим Xi от х^. Отсюда немедлепно вытекает теорема.

Повторно применяя неравенство (11.8) к потокам в скобках из (11.8), получим

fij>min[/is, /hft, fhn, .... fupj] (11.9)

для любой последовательности вершин Xi, х^ хи, жьд, . , х^ ,

Если теперь рассмотреть гипотетический полный граф G с п вершииами и взять в качестве длины ребра {хи, Xj) максимальный поток fij между соответствующими вершинами Xi и Xj из G, то эти длины можно использовать для построения длиннейшего остова Г* графа G, применяя один из методов построения кратчайшего (или длиннейшего) остова, приведенных в гл. 7. В соответствии с (11.9) можно сказать, что ноток fij больше или равен, чем длина кратчайшего ребра, лежащего на единственной цени в Т* из xi в xj. Если, однако, fij больше, чем длина кратчайшего ребра, то удаление этого ребра и добавление {х1, Xj) даст новое