Доказательство. Пусть с [] - стоимость потока в графе G, а с [Ф I (I)] - сумма стоимости цуг в цикле Ф по отношению к графу (I).

Необходимость. Пусть с [Ф G* ()] < О для некоторого цикла Ф из (I). Циркуляция дополнительной единицы потока по циклу Ф дает новый поток -f- 1 ° (Ф) оставляя значение v потока от s к f неизменным. Стоимость потока + 1 ° (Ф) равна с[\] + с [Ф] G (1)1 < с [], а это противоречит допущению, что I - поток минимальной стоимости со значением v.

Достаточность. Допустим, что в графе G (): [Ф G ()] О для каждого цикла Ф и что * (=?) - поток минимальной стоимости со значением v. Обозначим теперь через * - поток, значение которого на дуге (х;, Xj) равно tj -

Так как * и можно разложить в сумму потоков (от s v. t) по цепям в G, то построение унитарного графа G (см. разд. 2.4) для потока I* - I дает следующие полустепени вершин:

df (Xi)=rff (Xi), vxez.

Так как в соответствии с разд. 2.4 G* состоит из наборов конфор-мальных единичных потоков по циклам Ф^, Фз, . . ., Ф^ (например), то мы можем написать

I*-I = 1 о (ФО-Ь1 о (Фг)-Ь ...-t-1 о (Ф^).

Так как потоки 1 о (Ф;), i = 1, . . ., А;, попарно конформальны и нам известно, что поток * = -- 1 о (ф^) + ... [ 1 о (ф^), допустим, то любая сумма -- 1 о (Ф^) + . . . + 1 о (ф^) будет допустимой для любых Z, 1 Z А;. Таким образом, рассматривая поток I -Ь 1 о (Фх), получаем

с [ +1 ° (Ф1)] = с [] -Ь с [Ф1 \Gm>c [].

Рассмотрим теперь инкрементальный граф ( -- 1 о (Ф^)). Единственными дугами этого графа, стоимости которых уменьшились по сравнению с соответствующими стоимостями в графе G (I), являются те, которые будут обрашениями дуг в Ф^. Но, так как потоки 1 о (Ф^), 1 о (Фз), . . . конформальны, такие дуги не могут быть использованы ни одним из оставшихся циклов Фз, . . ., Фй и, следовательно, не влияют на последующие рассуждения.

Теперь мы имеем

с [Фг I а + Ь (Ф1))] > с 1Ф, I G* (I)]

для любого 1 = 2.....к.

Стоимость потока + 1 о (Oj.) + 1 о (ф^) равна тогда

с [ + 1 о (ф.) + 1 о (Фз)] = С [1 + 1 о (Ф,)] + С [Фг I Gl + 1 о (ф^))] >

>с [1+ 1 о (ФО] + с [Фг I (1)] >с [ +1 о (Ф,)]>с [].

Продолжая рассуждения аналогичным образом, мы получим окончательно с [%*] > с [], а это противоречит предположению о том, что %* - поток минимальной стоимости со значением v. Теорема доказана.

Таким образом, в соответствии с теоремой 5, все, что требуется для нахождения потока минимальной стоимости со значением и,- это начать с допустимого потока со значением v, построить граф G {%) и проверить, нет ли в нем циклов с отрицательной стоимостью, используя любой из алгоритмов нахождения кратчайшей цепи, данных в разд. 3 и 4 гл. 9. Если не существует никакого цикла с отрицательной стоимостью, то поток будет потоком минимальной стоимости. Если цикл Ф с отрицательной стоимостью существует, то надо пустить по нему поток с максимально возможным значением 6. Суммарный поток от s к f не изменит своего значения у, а его стоимость уменьшится на б с (Ф), где с (Ф) - величина стоимости отрицательного цикла. Очевидно, б должно быть выбрано так, чтобы пропускные способности дуг в (I) не превышались, т. е.

б= min [gf.]. (H.ll)

(xf, xf в Ф

Если этот поток б наложить на поток % уже в графе G, то, в силу первоначального выбора пропускных способностей дуг в Gt* (), результирующий поток все еще будет допустимым. Процесс можно повторять, начиная его с полученного нового потока , строя новый граф G () относительно нового потока и выявляя в этом графе циклы с отрицательной стоимостью. Описание алгоритма дано ниже.

5.1.1. Описание алгоритма

Шаг 1. Использовать алгоритм максимального потока (от s к f) из разд. 2 для нахождения в графе G допустимого потока со значением v.

Шаг 2. Построить для этого потока граф G {%), пользуясь данными ранее правилами.

Шаг 3. Отправляясь от матрицы стоимостей графа G () и используя алгоритм кратчайшей цепи (см. разд. 3.1 и 4 гл. 8), определить, существует ли в графе G () цикл с отрицательной стоимостью, Если такой цикл существует, то найти его (цикл Ф)

07,25)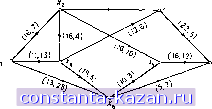

Рис. 11.13. Граф из примера 5.1.2. Первая пометка является пропускной способностью дуги, вторая - стоимостью дуги.

и перейти к шагу 5. Если такого цикла нет, то остановиться. Поток I будет потоком минимальной стоимости.

Шаг 4. По (11.11) вычислить б.

(I) Для всех {xf, х^) в Ф с cf. < О изменить поток в соот-ветствуюгцей дуге {xj, Xj) из G с /j на - 6.

(II) Для всех {xf, xf) в Ф с cW > О изменить поток в соот-ветствуюгцей дуге (х;, xj) из G с 1;; на + б-

Шаг 5. Повторить шаг 2, начиная с нового потока .

5.1.2. Пример. Рассмотрим граф G, изображенный на рис. 11.13, где первое число пометки у каждой дуги равно ее пропускной способности, а второе - стоимости. Мы хотим найтв поток 01 S к t минимальной стоимости со значением 20.

Для выявления циклов с отрицательной стоимостью на шаге I вышеописанного метода используем алгоритм кратчайшей цеш Флойда (разд. 3.1 гл. 8).

Шаг 1. Алгоритм максимального потока дает первый допустимый поток, изображенный на рис. 11.14а. Стоимость этого потокг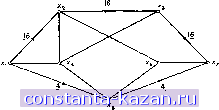

Рис. 11.14а. Начальный поток .