равна

16 (7 + 25 + 5) + 4 (28 + 7) = 732.

Шаг 2. Исходя из этого потока, построим граф (), как показано на рис. 11.146, где цикл отрицательной стоимости изображен пунктиром.

Шаг 3. Начиная с матрицы стоимостей

(где на пустых местах должны стоять элементы оо) и применяя алгоритм Флойда, получаем следующие матрицы наименьших стоимостей вместе с соответствующими им матрицами цепей:

Матрицы I конце перВой итерации (h=1)

Матрица иаименших стоимостей

Mampuufl цепей

в последней итерации элемент С4,4 получается отрицательным, со значением -15, которое показывает существование цикла отрицательной стоимости, содержащего вершину х^. Этот цикл, найденный по матрице цепей, имеет вид (4, Хз, х^, х^.

Шаг 4. Из (11.11) находим значение 6:

Ишприцы в конце Отрой итерации f/c-2l

Матрица иаименших cmoumcmei

Матрица цепей

Матрицы в конце mpemteu итерации (/i-3)

Матрица наименьших стоимостей

Матрии/г цепей

Новый поток, полученный после введения в цикл циркуляционного потока б, изображен на рис. 11,14в. Стоимость нового потока равна 552. Возвращаясь к шагу 2, находим новый граф (), показанный на рис. 11.14г. Поступая как и раньше, получаем

(16.-25)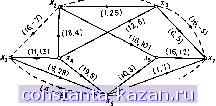

Рис. 11.146. G (I) для потока на рис. (а)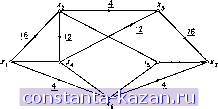

Рис. 11.14в. Улучшенный поток 5. (4,-25)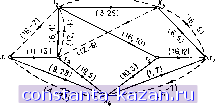

Рис. 11.14г. G (I) для потока на рис. (в).