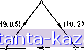(15,1) *2 (2,1,5) (а)

(6,3)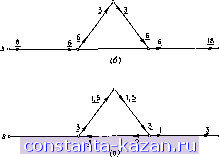

5 7

Рис. 11.16. (а) Граф G: первая пометка - пропускная способность дуги, вторая - выигрьпп дуги, (б) Максимальный поток, (в) Оптимальный поток, (г) Оптимально-максимальный поток.

(I) поток, изображенный на рис. 11.16 б, является максимальным потоком со значениями г; = 18 и г; = 6;

(II) поток, изображенный на рис. 11.16 в, является оптимальным потоком со значениями = 3 и Us = О (заметим, что поток порожден циркуляцией по циклу, у которого полный выигрыш больше чем 1; кроме того, vt < Vf и, следовательно,

поток не является максимальным, но у< представляет собой максимум, который может быть получен при Vs = 0);

(III) поток, изображенный на рис. 11.16 (г), является оптимально-максимальным, имеющим Vt = Vt, но i; = 5 <; = 6 и, как будет показано ниже, наименьшее возможное значение у дающее выходной поток со значением 18, равно 5.

6.1. Аугментальные маршр^чш

Рассмотрим граф с выигрышами, в котором существует допустимый поток S = (I*, 1°). Обозначим этот граф через G (S), Маршрут (не обязательно цепь от вершины к вершине x называется аугменталъным маршрутом от к Xjj, если в графе G (S) по этому маршруту можно послать поток от xt к Ж;;. (Это аналогично определению аугментальной цепи потока (от s к t) в задаче о максимальном потоке (от s к t).) Если маршрут задан последовательностью вершин Xi, Xi , . . ., ж,- , то пусть F - множество всех прямых дуг в нем (т. е. дуг {xi, xi) с Xi 6 6 Г (xi )) и Б - множество всех обратных дуг (т. е. дуг, для которых Xi 6 Г {xi )). Маршрут является аугментальным, если . < для каждой прямой дуги (Xj, xj) f-a , > О для каждой обратной дуги {Х], Xt) 6 В.

А. Выигрыш маршрута. Выигрыш маршрута S = (xj Х|) определяется так:

g(S)= П gtr П ilgjf (11.15)

Б. Пропускная способность маршрута.

Инкременталъная пропускная способность аугментального маршрута S равна значению такого максимального входного потока в вершине Xj , который может быть послан по данному маршруту к вершине Xi и либо насыщает поток в некоторой прямой дуге из S, либо обращает в нуль поток в некоторой обратной дуге маршрута S.

Если S - цепь и в Xi входит ноток величины б, то входной поток (в вершине Xj) на дуге (xj, Xi) из S равен

Smp.. = 6- П gw П 1/я = б.(5Д (11.16)

(x Xj)Fj, (Xj,Xi)£Bp

где Fj, а Bp - множества соответственно прямых и обратных дуг Л8 подцепи Sp = (Xi, Xj, . . ., Xj) и g {Sp) - выигрыш цени S,.

x, (8,7)

>2 0S.3) \/Хз (9А2) \/Х4 (12.0,5) 5

2(У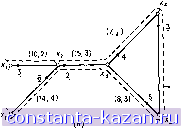

(12,2)

Цепь S

Общий входной поток: 2+2(У-Зс?=2-<У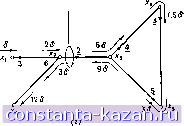

Рис. 11.17. (а) Цепь S с начальными входными потоками, показанными подчеркнутыми числами: первая пометка в скобках - пропускная способность дуги, вторан - выигрыш дуги, (б) Цепь S с введенным дополнительным потоком, (в) Маршрут S с начальным входным потоком, показанным подчеркнутыми числами: первая пометка в скобках - пропускная способность дуги, вторая - выигрыш дуги, (г) Маршрут S с введенным дополнительным потоком.