где F ти В, как и прежде,- множества прямых и обратных дуг цикла Ф.

Если g (Ф) > 1, то log [g (Ф)] > О, откуда следует, что

стоимость цикла Ф в (S), т. е. 2 ij + 2 cf;, должна быть отри-

F в

цательной. Обратно, если (Ф)1, то стоимость цикла Ф в С (S) неотрицательна.

Таким образом, активные циклы в G (S) - на шаге 2 вышеописанного алгоритма - могут быть определены посредством нахождения всех кратчайших (наименьшей стоимости ) цепей, идуш,их из вершин графа (S) к конечной вершине t (для чего можно воспользоваться методом из разд. 2.2.1 гл. 8, как это было объяснено в разд. 4 настояш,ей главы), и проверки циклов на отрицательную стоимость. Если, однако, поток б, циркулирующий по активному циклу Ф на шаге 3 и передаваемый по аугмептальному маршруту к t, не уменьшает до нуля пропускную способность самого цикла Ф, а вместо этого уменьшает до нуля пропускную способность аугментальпого маршрута, то при следующем выполнении шага 2 нужно только найти другой аугментальный маршрут, ведущий из вершины цикла Ф в вершину t. Такой маршрут снова сделает цикл активным и можно будет перейти к шагу 3 и т. д. вплоть до того момента, когда цикл Ф дезактивируется. Тогда на шаге 2 ищется некоторый другой активный цикл.

Шаг 5 вышеописанного алгоритма также можно выполнить с помощью метода разд. 2.2.1 гл. 8, так как он состоит просто в вычислении кратчайшей цепи от s к f в графе G* (S). Этот граф освобождается от циклов отрицательной стоимости, как только выполнены четыре предыдущие шага алгоритма.

6.4. Пример

Мы хотим найти оптимально-максимальный поток от вершины Ху к вершине Xg в графе на рис. 11.18, где первое число у дуги

(15,1)

(8,2)

(3,1)

-3 (8,0,5) ЛГ, (15,6,75) Хе (9,7) Xj

Рис. 11.18, Граф из примера 6.4. Первая пометка - пропускная способность дуги, вторая - выигрыш дуги.

S=x,

4,5(У

XriZS

1,5 <f

Рис. 11.19a. Поток после 1-го этапа. - насыщенная дуга.

3 X,f

Хз Х4 3 2,625 2.625 5,25 X7

Рис. 11.196. Поток после 2-го этапа. - насыщенные дуги.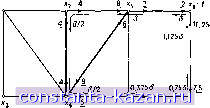

3 Xg 3 JX

Рис, 11.19в. Поток после 3-го этапа, насыщенные дуги.

S=x,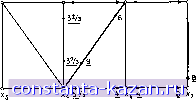

Рис. 11.19. г. Оптимальный поток. - насыщенные дуги.

является ее пропускной способностью, а второе - ее выигрышем.

Начиная с S = (О, 0) находим первый активный цикл Ф = = (xg, Х4, Х2, Х5) с аугментальным маршрутом (xg, Xg). Циркуляция потока б (где б - входной поток дуги (xg, Х4)) по этому маршруту, как показано на рис. 11.18, дает максимальный допустимый поток со значением 6=1,5, и для этого значения получающийся поток показан (подчеркнутыми числами) на рис. 11.19а, причем дуга (xg, Xg) насыщена. Пропускная способность самого цикла не уменьшается до нуля, и поэтому при следующей итерации, когда алгоритм кратчайшей цепи (действующий от всех других вершин графа G* (S) к вершине t) помечает вершину х, из Ф, цикл Ф снова становится активным с новой аугментальной цепью (Х4, Xg, Х7, Xg). Посылая поток б по циклу и передавая его по аугментальной цепи к f, как показано на рис. 11.19а, получаем поток, изображенный на рис. 11.196 подчеркнутыми числами.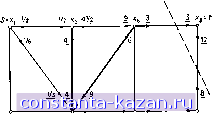

Х4 5Vs ±Хе ± 8 Ху

Рис. И.19д. Оптимально-максимальный поток. - насыщенные дуги.