1 То есть рассматриваются только пути, длины которых не превосходят q.- Прим. ред.

фа G*, т. е.

B, = J. (2.8)

Для графа, приведенного в примере 4.1 (рис. 2.2 и 2.3), сильная база G есть {х^, Жц, х^, Xjs}. Можно отметить, что, если этот граф представляет организацию, то х^ можно рассматривать как руководителя, обладаюп1;его властью над всеми множествами лиц X*, Х2 и X*, в то время как {жц, х^, х^} можно рассматривать как комитет, имеюп1;ий власть над двумя множествами лиц ж! и ж|.

5. Задачи, связанные с ограниченной достижимостью

В предыдуп1;ем разделе при определении базы мы исходили из неограниченных достижимых множеств. Если рассматривать ограниченную достижимость, т. е. использовать пути ограниченной длины (как упоминалось ранее в разд. 2), и определят!, ограниченную базу, опираясь на ограниченную достижимость, то возникают осложнения двух типов.

(а) Понятия сильной компоненты и конденсации, которые упроп1;ают решение задачи определения баз в случае неограниченной достижимости, теперь использоваться не могут. Распространение этих понятий на случай ограниченной достижимости не дает суп1;ественного упроп1;ения задачи.

В случае когда достижимость ограничена путями единичной длины (просто дугами), ограниченные базы называют минимальными доминирующими множествами. Мы подробно рассматриваем их в гл. 3. В случае когда достижимость ограничена, скажем, q дугами ), граф G может быть определен как граф, множество вершин которого то же самое, что и у графа G, а дуга (ж;, Xj) суп1;ествует в G тогда и только тогда, когда в G найдется путь между вершинами Xi и Xj длины, не больше чем q (см. соотношение 2.1). Ограниченная матрица достижимостей графа G соответствует тогда матрице смежности графа G; граф G может быть назван ограниченным транзитивным замыканием графа G (в соответствии с определением транзитивного замыкания, приведенным в разд. 2). Задача определения ограниченных баз графа G эквивалентна задаче нахождения минимальных доминируюп1;их множеств графа G.

(б) В неограниченном случае различные базы имеют одно и то же число элементов; оно равно числу таких вершин в конденсации графа, которые имеют нулевые полустепени захода. В огра-

яиченном случае, однако, разные базы могут иметь различное число элементов, и тогда возникает, в частности, задача нахождения базы с наименьшим числом элементов. Еще один подход: если не наложено ограничение на достижимость, то можно искать такую ограниченную базу, которая содержит, например, ровно р вершин и, кроме того, из вершин этой базы все остальные вершины графа G могут быть достигнуты с минимально возможной ограниченностью достижимости. Эти задачи тесно связаны с задачей нахождения р-центра и более детально рассматриваются в гл. 4.

6. Задачи

1. Для графа, приведенного на рис. 2.4, найти матрицы достижимостей и контрадостижимостей.

2. Для графа, приведенного на рис. 2.4, найти сильные компоненты, начертить конденсацию и построить все его базы.

3. Доказать, что в любом графе G каждая его база содержит все вершины, имеющие нулевые полустепени захода.

4. Доказать, что в любом графе без циклов имеется только одна база. Она состоит из всех вершин с нулевыми полустепенями захода.

5. Показать, что любые две базы графа G имеют одно и то же число вершин.

6. Доказать, что вершина Xi принадлежит одновременно базе В и антибазе В графа G тогда и только тогда, когда сильная компонента, содержащая х,-, соответствует изолированной вершине в конденсации G*.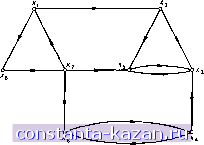

Рис. 2.4.

7. Список литературы

1. Chen Y. С, Wing О. (1964), Connectivity of directed graphs, Ргос. of Allerton Conference on Circuit and System Theory, Univ. of Illinois.

2. Flament C. (1963), Applications of graph theory to group structure, Prentice-Hall, Englewood Cliffs, New Jersey.

3. Harary F., Norman R. Z., Cartwright D. (1965), Structural models: An introduction to the theory of directed graphs, Wiley, New York.

4. Лейфман Л. Я. (1966), Эффективный алгоритм разбиения ориентированного графа на бикомпоненты, Кибернетика, 2, стр. 19.

5. Marimont R. В. (1959), А new method of checking the consistency of precedence matrices, /. of ACM, 6, p. 164.

6. Moyles D. M., Thompson G. L. (1969), An algorithm for finding a minimum equivalent graph of a digraph, /. of ACM, 16, p. 455.

7. Ramamoorthy C. V. (1966), Analysis of graphs by connectivity considerations, /. of ACM, 13, p. 211.

7. Показать, что если Xt есть такая вершина графа {X, А), на которой достигается

max I R (Xf) I,

то Xi принадлежит базе.

8. Пусть все арифметические операции, рассматриваемые ниже, являются булевскими (т. е. 0-fO = 0, 0-(-1 = 1--0 = 1, 1 + 1 = 1, 0-0 = 0-1 = О и 1-1 = 1). Показать, что если рассматривать достижимость только на путях длины не больше чем q, то матрица ограниченных достижимостей дается формулой

Rg = I + A-fA2-f ... -f А'-(1 + А), где I - единичная {п X ге)-матрица.

9. Показать, что элемент r\f матрицы R равен числу вершин в сильной компоненте, содержащей вершину ж,-.