Новый активный цикл (xg, Xg, х^, а; х^, х^ определяется на шаге 2, и циркуляция потока б по этому циклу, как показано на рис. 11.19(6), дает ноток, изображенный подчеркнутыми числами на рис. 11.19(b). Наконец, определяется активный цикл (Xg, Хб, а;4, Xg, х^, Xg) и его дезактивация с номош,ью циркуляции потока приводит к потоку, изображенному на рис. 11.19г. Последний будет оптимальным потоком, так как больше не удается обнаружить никаких активных циклов.

Аугментальный маршрут (от s к f) с максимальным выигрышем есть (xi, Х4, Xj, Хб, Xg) с иронускной способностью Ve. Как только этот маршрут будет насыш,ен (дуга (Х4, х^) уже насыш,ена), аугментальным маршрутом со следуюш,им наибольшим выигрышем будет (xi, Xj, Х5, Xg), и он носле насыш,ения даст ноток на рис. 11.19д. Этот ноток будет требуемым оптимально-максимальным потоком, так как больше нельзя найти никаких аугментальных цепей (от s к t).

6.5. Г рафы с выигрышами в вершинах

Задача о максимальном потоке (от s к f) для случая, когда пропускными способностями обладают вершины, была решена в разд. 3.2 с помощью простой замены каждой вершины Х] нарой вершин Xj и xJ. Аналогичным образом, если вершинам графа G иринисаны выигрыши и, следовательно, условия (11.14) ненре-рывности потока не выполняются, то мы можем образовать другой граф Go, заменяя каждую вершину Xj нарой вершин х\ и xJ с дугой (х|, xJ;) между ними. Выигрыш этой дуги считается равным выигрышу вершины Xj. Для дуги (xj, Ху) из G мы тогда имеем дугу (хГ, Xj) в Go, а для дуги (ху, х^) из G - дугу (xJ, xt) в Gq. Задача носле этого сводится к нахождению оптимальных потоков в графе Gq, в котором выигрыши приписаны только дугам.

7. Задачи

1. Найти максимальный поток * от х^ к х, в графе, изображенном на рис. 11.20, где иронускные способности дуг указаны стоящими около них числами.

2. Начертить инкрементальный граф G** () для примера из задачл 1.

3. Разложить поток, найденный в задаче 1, на элементарные потоки (от S к f) по цепям и циклам.

4. Пусть в графе, изображенном на рис. 11.20, потоки по дугам (xj, Хз), (хб, Х4) и (ха, Хб) ограничены снизу значениями Ггз = 4, Гб4 = 7 и г^Б = 3 соответственно. Найти максимальный ноток от Хх к Х7 или показать, что такой поток не существует.

5. Доказать теорему 3 из разд. 3.3.

6. Найти максимальные потоки между всеми парами вершин для графа G, изображенного на рис. 11.21, и начертить потоково-эквивалентное дерево. Определить разрезы в G, соответствующие этому потоково-эквивалентному дереву. Найти два других пото-ково-зквивалентных дерева.

7. Найти максимальный поток с минимальной стоимостью от ХуК XgB графе на рис. 11.22, если первое число у дуги равно ее пропускной способности, а второе - стоимости.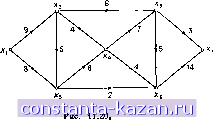

8. Какие упрощения могут быть сделаны в алгоритме потока минимальной стоимости в случае, когда требуемое значение потока является максимально возможным?

9. В алгоритме максимального потока (от s к f) из разд. 2.1 среди многих возможностей, возникающих при выборе аугментальных цепей, две таковы:

(I) выбирается аугментальная цепь с наименьшим числом дуг, (И) выбирается та цепь, которая позволяет послать от s к f аугментальный поток с максимально возможным значением б.

Какая из этих двух возможностей предпочтительнее в вычислительном отношении и как зависят они от величины пропускной способности дуг? (см. [9]).

10. Доказать теорему 6 из разд. 5.2.

11. Доказать теорему 7 из разд. 6.2.

12. В графе, изображенном на рис. 11.23, найти оптимальный, максимальный и оптимально-максимальный потоки, если первое число, стоящее у дуги, равно ее пропускной способности, а второе - ее выигрышу.

гл. и. потоки в СЕТЯХ

Рис. 11.21.

(2,25)

(4,6)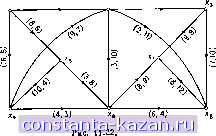

, (3,0

х, (7,1) Х4 (9,С,5; Xj Рис. 11.23.