На рис. 12.1 (а) паросочетание в графе показано жирными линиями, а на рис. 12.1 (б) в том же самом графе жирными линиями показано покрытие.

В частном случае, когда веса всех ребер равны единице, ЗМП и ЗПО сводятся к задаче о наибольшем паросочетании (ЗНПС) в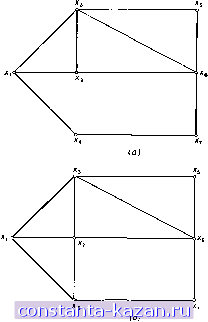

Рис. 12.1. (а) Паросочетание. (б) Покрытие.

задаче о покрытии наименьшей мощности (ЗПНМ). Если граф G имеет п вершин, то число ребер в паросочетании графа G не может, очевидно, превышать величины [п/2]. Однако это число не всегда достигается; например, для звездного графа на рис. 12.2 наибольшее число ребер в паросочетании равно 1.

В том специальном случае, когда веса Cj произвольны, а сам граф является двудольным, задача о максимальном паросочетании

сводится к задаче о назначениях (ЗН) - задаче, очень хорошо известной в исследовании операций. В графе такой специальной структуры общая задача превращается в другую хорошо известную задачу - транспортную задачу (ТЗ).

В настоящей главе мы дадим эффективные методы решения ЗМП ЗПО, ЗН и ТЗ. ЗМП возникает в качестве подзадачи в задаче об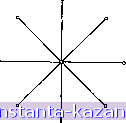

Рис. 12.2. Звездный граф.

обходе графа и в задаче китайского почтальона. Последние встречаются в задачах распределения, таких, как доставка молока и почты, посыпка зимой дорог смесью соли и песка, сбор мусора (см. гл. 9). ЗН и ТЗ являются двумя основными задачами с многочисленными прямыми и косвенными приложениями в самых различных областях, часто весьма далеких от тех областей, на которые указывают названия этих задач.

2. Наибольшие паросочетания

Если дано паросочетание ikf, то вершина Xi, не являющаяся конечной вершиной никакого ребра из ikf, будет называться экспонированной вершиной. На рис. 12.3, где паросочетание показано жирными пиниями, вершины х^ и х^ являются экспозирован-ными.

2.1. Альтернирующие цепи и деревья

Альтернирующая относительно М цепь - это простая цепь ребра которой попеременно лежат или не лежат в паросочетаний М. Примером такой цепи является цепь (Xg, Ху, Хб, х^, х^, х^, Ху} в графе на рис. 12.3. Аугментальная относительно М цепь - это такая альтернирующая цепь, начальная и конечная вершины

которой экспонированы. Цепь (х Хю, х^, х^, х^, Хз, х^, Xj) дает пример аугментальной цепи в графе, изображенном на рис. 12.3.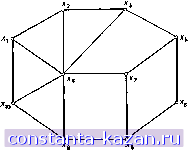

Рис. 12.3. Паросочетание М.

Основная относящаяся к паросочетаниям теорема может быть сформулирована так.

Теорема 1 [5, 27]. Паросочетание М будет наибольшим паросочетанием тогда и только тогда, когда в G не cyuecmsyem никакой аугментальной относительно М цепи.

Доказательство. Необходимость. Допустим, что существует аугментальная цепь Р, и пусть Р обозначает также множество ребер этой цепи. Никакое ребро в множестве М - Р [\ М лв может быть смежным ни с каким ребром в Р, так как две концевые вершины в Р являются (по определению) экспонированными, а каждая другая вершина в Р уже является концевой вершиной некоторого ребра ъ Р {\ М. Следовательно, множество ребер М' = = (М - РП М)\}{Р - Р{\М) = М\} р - р [\ М, полученное в результате замены тех ребер из Р, которые не входят в М (т. е. ребер из множества Р - Р [\ М), на ребра из Р, которые входят в М (т. е. на ребра из Р П является паросочетанием. Но так как оба концевых ребра из Р не лежат в М, то Р - Р П М содержит на одно ребро больше, чем Р [\ М, и поэтому М' = = I М I -f 1, так что М не является наибольшим паросочетанием.

Достаточность. Пусть М - паросочетание, относительно которого нет ни одной аугментальной цепи в графе G, и пусть М* - наибольшее паросочетание. Построим остовный подграф Gp, образованный ребрами из М и М* - МП М* вместе с соответствующими им вершинами. Никакая вершина из Gp не может иметь