степень, большую чем 2, так как в противном случае два или более ребер из М (или М*) являются смежными, что противоречит определению паросочетания. Таким образом, подграф Gp состоит из одной или более компонент, и каждая из них есть либо изолированная вершина, либо простая цепь, либо простой цикл, как это изображено на рис. 12.4.

Цепь типа (б) существовать не может, так как она является аугментальной цепью относительно М, это противоречит перво-

(tf, ---&

Xq Х^

Xq Xf.

Сд) X,

- Ребра----Ребра

ъ М в М*

Рис. 12.4.

начальному предположению. Цепь типа (в) не может существовать, так как она является аугментальной относительно М*, что противоречит предположению о максимальности М*. Цикл типа (д) с нечетным числом ребер не может существовать, так как тогда либо два ребра из М, либо два ребра из М* были бы смежными друг с другом. Остаются возможными графы следуюпщх видов: (а), (г) и циклы типа (д) с четным числом ребер. Для каждого из таких графов число ребер п (М) в М равно числу ребер п (ikf *) в М*. Так как это справедливо для любой связной компоненты к

графа Gp, то

где Hk (М) и (М*) - число ребер в компоненте к, принадлежащих соответственно М и М*. Поэтому

л, следовательно, М - наибольшее паросочетание.

Рассмотрим в качестве примера граф, изображенный на рис. 12.3. Ребра, образующие паросочетание М в этом графе, выделены жирными линиями. Множество ребер в аугментальной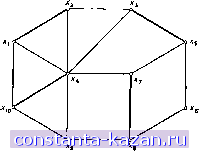

Рис. 12.5. Наибольшее паросочетание М'.

щепи Р = (xg, XiQ, Xi, X2, Хз, Хъ, x), не лежащих в М, дает новое паросочетание М', изображенное на рис. 12.5. Здесь уже нет экспонированных вершин и поэтому не существует никаких аугментальных относительно М' цепей. Следовательно, по теореме 1 М' - наибольшее паросочетание.

Альтернирующим деревом относительно данного паросочетании М называется дерево Т, для которого

(а) одна вершина, называемая корнем дерева Т, является экспон ированной;

(б) все начинающиеся в корне цепи являются альтернирующими;

(в) все максимальные цепи, начинающиеся в корне дерева Т, содержат четное число рёбер.

Разобъем все вершины дерева на два класса: Ф - класс внешних вершин, / - класс внутренних вершин. Корень дерева отнв-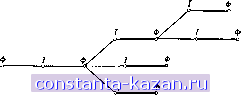

Рпс. 12.6. Альтернирующее дерево. / - внутренние вершины, Ф - внешние вершины.

С условием (в) будут внешними . Степень любой внутренней вершины альтернирующего дерева равна 2, в то время как степень внешней вершины может быть любым целым положительным числом.

Аугменталъное дерево - это альтернирующее дерево относительно данного паросочетания, удовлетворяющее условию; существует ребро от какой-нибудь внешней вершины дерева Хд, до некоторой экспонированной вершины Хе, не принадлежащей дереву. Единственная цепь, идущая от корня дерева до вершины Хд и далее - по ребру {х^, е^), будет тогда аугментальной цепью.

2.2. Цветки

Цветком по отношению к паросочетанию М называется аугментальная цепь, начальная и конечная экспонированные вершины которой совпадают, т. е. эта цепь является циклом, так как число ребер этой цепи нечетно. На рис. 12.7 изображен цветок, образованный цепью с 5 ребрами.

В алгоритмах для ЗМП и ЗНПС, описанных ниже, цветки срезают для того, чтобы получить более простой новый граф. Срезание цветка В состоит в замене всех вершин цветка В (скажем, Хв) одной новой псевдовершиной Хь- Ребро {х^, х^) добавляется всегда, когда существует ребро из некоторой вершины Xi 6 Xg к другой вершине х^ $ Хв- В упрощенном графе, полу-

сен к классу Ф. Вершины вдоль любой цепи, начинающейся в корне, будут поочередно отнесены к классам Фи/. Таким образом, если вершина расположена в конце цепи с нечетным числом ребер, начинающейся в корне, то эта вершина будет отнесена к /, а если она лежит в конце цепи с четным числом ребер, начинающейся в корне, то будет отнесена к Ф. На рис. 12.6 изображено альтернирующее дерево. Здесь все вершины, лежащие в конце максимальных цепей, начинающихся с корня, в соответствии