ченном после срезания, вершина и другие псевдовершины, соответствующие ранее срезанным цветкам, могут в свою очередь образовывать новый цветок, который опять срезается, и т. д. Последний цветок В^, не содержащийся ни в каких других цветках, называется крайним цветком. Обоснование процесса срезания цветков основано на теореме 2, приводимой ниже.

Цветущее дерево - это альтернирующее дерево относительно данного паросочетании, для которого существует ребро {х'о, xl), соединяющее две внешние вершины дерева: х'о и xl. Если Р' - множество ребер цепи, начинающейся в корне альтернирующего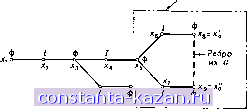

Рис. 12.7. Дерево с цветком.

дерева и кончающейся в х'о, а Р - соответствующее множество для xl, то множество ребер {Р' U Р - Р' {] Р \ вместе с ребром {х'о, х'о) образует цветок. На рис. 12.7 изображено цветущее дерево.

Когда цветок В срезан, получающаяся псевдовершина считается внешней вершиной. Всякая вершина из В может быть по желанию отнесена к внутренним или к внешним вершинам, так как если вершина принадлежит В, то она является концевой и в цепях с четным, и в цепях с нечетным числом ребер, начинающихся в корне дерева (в зависимости от маршрута, по которому проходят эти цепи до прихода в первую верпшну цветка). Так, на рис. 12.7 вершина х^ может быть помечена как внутренняя, если рассматривать цепь {х-, х^, Хз, х^, х^, Xg), и как внешняя, если брать цепь {xi, Х2, Xg, х^, х^, х. х^, х^, х^). Но когда псевдовершина, получающаяся после срезания цветка, помечается как внешняя , структура остающегося альтернирующего дерева все еще будет корректной - как это вытекает из определения альтернирующего дерева. Таким образом, после срезания цветка альтернирующее дерево в получившемся графе сохраняется.

Пример сложной формации цветков и их срезание показаны на рис. 12.8а - 12.8г. В графе на рис. 12.8а паросочетание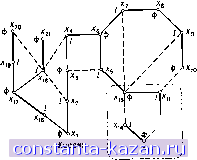

Рис. 12.8а. Срезание цветка В^.

- Ребра в альтернирующем дереве, входящие в паросочетание.

- Ребра в альтернирующем дереве, не входящие в паросочетание

---Другие ребра графа.

изображено жирными линиями. Альтернируюш;ее дерево Т с корнем в экспонированной вершине показано сплошными линиями, а все другие ребра графа, не входяш;ие в дерево Т,- пунктиром. Допустим, что последнее добавленное к дереву ребро есть {хц, Ж12). Так как между двумя внешними вершинами xz и х-з существует ребро, то добавление к дереву вышеупомянутого последнего ребра дает цветок. Цветок By, обведенный на рис. 12.8а штрих-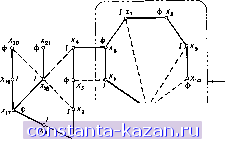

{Х„,Х,2,Х,з,Х,4,Х,

Ьх, Корень Рис. 12.86. Срезание В^.

Цветок В,

пунктирной замкнутой линией, после срезания дает псевдовершину хы. как это показано на рис. 12.86. Дерево на рис. 12.86 все еще является цветущим с цветком В2, так как существует ребро (хщ, Xbi). После срезания цветка В2 остается вершина Хь2 и получается новый граф, изображенный на рис. 12,8в. Дерево на рис. 12.8в опять будет цветущим ввиду существования ребра {хз, Xbi); цветком в нем будет В3. После срезания цветка

(A5,Xs,...,X,5}J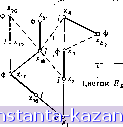

---?Xt

Рис. 12.8в. Срезание В^.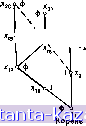

Рис. 12.8г. Альтернирующее дерево после срезания цветков.

-Вз остается вершина хь, и граф, изображенный на рис. 12.8г. Больше цветков нет, и, значит, Вз будет крайним цветком.

Теорема 2. Если В - цветок с нечетным множеством вершин Хв и если X - некоторая вершина из Хв, то в подграфе (Хв) существует наибольшее паросочетание, для которого вершина X будет экспонированной.

Доказательство. Пусть {х^, х^, . . ., х„) - цикл с нечетным числом ребер, образуюшдй цветок В. Тогда или х = xt для некоторого i = 1, 2, . . ., а, или же X Xi для некоторой псевдовершины Xi, соответствующей ранее срезанному цветку 5;.

В первом случае вершина х может быть оставлена экспонированной, а остальные а - 1 вершин из В разбиваются на пары, образуя паросочетание. Такое разбиение возможно, так как а - 1 - четное число вершин, остающихся в цикле (после выбора вершины х). Если одна из этих вершин, скажем х^, соответствует ранее срезанному цветку В^, то вхождение в паросочетание будет означать возможность разбиения на пары всех вершин из Bp, кроме одной, а одна уже использована на предыдущем шаге. Этот процесс можно продолжить до тех пор, пока все вершины (отличные от х) не будут разбиты на пары, образуя паросочетание.