Oj и Pft и пометки будут такими:

Пометки делаются в следующем порядке: Рстолб з =/столб 4 = = 1, /?стрз = 3 (или 4), Рстр2 = 4, Рстолб5 = 2, после чего помечен столбец 5 с Ps = 2 и найдена аугментальная цепь (показанная выше). Вычисленное е равно 2, и после шага 7 матрица такова:

6. Задача о покрытии

Задача о покрытии наименьшей мош,ности (ЗПНМ) была сформулирована во введении, и она состоит в нахождении такого множества Е ребер графа G = (X, А), что число ребер в Е минимально и каждая вершина из G является концевой вершиной по крайней мере одного ребра из Е. Теперь, основываясь на следующей теореме, мы покажем, что ЗПНМ и ЗНПС эквивалентны.

Теорема 6. Если Е* - наименьшее покрытие и если для каждой вершины Xi со степенью di > 1 удалить все ребра, инцидентные Xi, за исключением одного, то оставшееся множество ребер М* будет наибольшим паросочетанием.

Доказательство. Так как в вышеприведенной конструкции df*i, то никакие два ребра в М* не будут смежными и М* является паросочетанием. Поэтому достаточно показать, что М* - наибольшее паросочетание. Допустим, что М* \ не максимально. Тогда по теореме 1 существует некоторая аугментальная цепь из какой-нибудь экспонированной вершины х, (т. е. вершины с di* = 0) к другой экспонированной вершине х^. Так как d* = = d* = О, то отсюда вытекает, что по крайней мере одно ребро, ведущее от Х; к другой вершине (=7 х^), можно удалить, и то же относится к вершине х^. Пусть одно из удаленных ребер, инцидентных Xi, будет а^, а одно из удаленных ребер, инцидентных Лй, будет а^. Пусть Р - аугментальная цепь (с 2р + 1 ребрами) от Xi к Xk- Если теперь удалить из Е* ребра из М*, принадлежащие цепи Р, и два ребра а^ и а^, то оставшееся множество (скажем, Е) все еще будет покрытием, так как каждая вершина из Р будет концевой для некоторого ребра из множества Е*. Но Е получено удалением из р + 2 ребер и добавлением р + 1 ребер; следовательно, I £ 1 < I * . Это противоречит предположению о том, что Е* - наименьшее покрытие. Значит, М*, построенное в соответствии с теоремой, является наибольшим паросочетанием.

Следующая теорема аналогична теореме 6 и точно так же доказывается [30].

Теорема 7. Если М* - наибольшее паросочетание графа G и для каждой экспонированной вершины Xi добавить ребро.

На шаге 2 алгоритм заканчивает свою работу, так как все г = О и решение в вышеприведенной матрице показано отмеченными элементами. Для этой ТЗ минимальная стоимость равна

3 X 3-Ь2 X 5 + 2 X 2 + 2 X 2 + 3 X 3+3 х 4 = 48.

7. Задачи

1. Найти наибольшее паросочетание графа, изображенного la рис. 12.26. Построить затем наименьшее покрытие этого графа.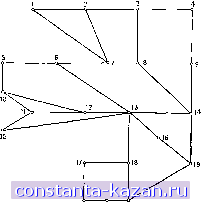

20 21 22 Рис. 12.26.

2. Найти максимальное паросочетание графа, изображенного а рис. 12.27, где числа у ребер являются стоимостями (весами).

3. Показать, что в двудольном графе G = (Х \J Х', А) овершенное паросочетание существует тогда и только тогда, огда для каждого SczX, iS Г (iS) . (Этот результат звестен как теорема Кёнига и Холла [5].)

4. Для графа, изображенного на рис. 12.28, найти какой-либо стовный подграф Gp, степени вершин которого задаются векто-ом [б;] = [1, 2, 1, 2, 3, 1, 3, 2].

тцидентное Xt, то получившееся множество ребер Е* будет наименьшим покрытием графа G.

Общая ЗПО, когда каждому ребру приписана некоторая стоимость, здесь обсуждаться не будет. Она может быть решена с помощью алгоритма, очень похожего на алгоритм для ЗМП. Подроб-1ый алгоритм для ЗПО дал Уайт [301.