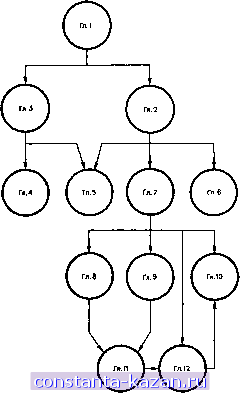Взаниосвязь между главами книги.

Глава 1 введение

1. графы. определение

Граф G задается множеством точек или вершин х^, х^, . . ., а; (которое обозначается через X) и множеством линий или ребер а^, . . ., а^ (которое обозначается символом А), соединяющих между собой все или часть этих точек. Таким образом, граф G полностью задается (и обозначается) парой (X, А).

Если ребра из множества А ориентированы, что обычно показывается стрелкой, ТО они называются дугами, и граф с такими ребрами называется ориентированным графом (рис. 1.1(a)). Если ребра не имеют ориентации, то граф называется неориентированным (рис. 1.1(6)). В случае когда G = {X, А) является ориентированным графом и мы хотим пренебречь направленностью дуг из множества А, то неориентированный граф, соответствующий G, будем обозначать как ) G = {X, А).

В ЭТОЙ книге, когда дуга обозначается упорядоченной парой, состоящей из начальной и конечной вершин (т. е. двумя концевыми вершинами дуги), ее направление предполагается заданным от первой вершины ко второй ). Так, например, на рис. 1.1(a) обозначение {xi, Х2) относится к дуге а^, а {х2, Х]) - к дуге aj.

Другое, употребляемое чаще описание ориентированного графа G СОСТОИТ в задании множества вершин X и соответствия Г, которое показывает, как между собой связаны вершины. Соответствие Г называется отображением множества X в X, & граф в этом случае обозначается парой G = {X, Г).

Для графа на рис. 1.1(a) имеем Г (ху) = {х2, х^}, т. е. вершины Х2 и х^ являются конечными вершинами дуг, у которых начальной вершиной является х^.

Г{Х2)={ХиХз},

Г{х,)={х,},

Г (х^) = 0 -пустое множество, Т(х,)={х,).

) Граф G мы будем называть неориентированным дубликатом (или неориентированным двойником) графа G.- Прим. ред.

Если II и I2 - концевые вершины дуги а, то говорят, что вершины Zi и Z2 инцидентны дуге а (или что дуга а инцидентна вершинам и х^.- Прим. ред.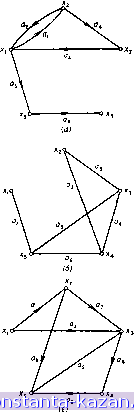

Рис. 1.1. (а) Ориентированный граф. (б) Неориентированный граф. (в) Смешанный граф.

В случае неориентированного графа или графа, содержащего и дуги, и неориентированные ребра (см., например, графы, изображенные на рис. 1.1(6) и 1.1(b)), предполагается, что соответствие Г задает такой эквивалентный ориентированный граф, который