Наименьшее доминирующее множество вершин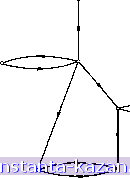

Наименьшее доминирующее множество ребер

(наименьшее покрытие)

ЗНП с единичными стоимостями

Наибольшее независимое множество

Наибольшая клика

Наибольшее независимое множество . (наибольшее паросочетание)

Рис. 3.5. Диаграмма взаимосвязей между задачами.

Наибольшие паросочетания и наименьшие покрытия можно описать на языке ЗНП. В случае покрытий столбцы матрицы Т представляют ребра графа G, а строки - его вершины, причем tij = 1, если вершина х, инцидентна ребру Uj, а иначе tij = 0. Следовательно, матрица Т в этом случае есть матрица инциденций графа G.

На рис. 3.5 показана диаграмма взаимосвязей между задачами, где дуга от задачи а к задаче Р означает, что решение задачи а влечет за собой решение задачи Р [34, 39]. Связь между наибольшими независимыми множествами вершин и наибольшими кликами устанавливается с помощью дополнительных графов, а между наибольшими независимыми множествалш вершин и наибольшими паросочетаниями - с помощью реберных графов. (Определение реберного графа см. в гл. 10).

5.6.4. Покрытие графа подграфами. Известно целое семейство задач, связанных с покрытием (или разбиением) множества вершин или множества ребер графа специальными подграфами (на специальные подграфы). Например, можно рассматривать порожденные подграфы или остовные подграфы графа, имеющие предписанные свойства. Тогда в матрицах Т из соответствующих ЗНП (или ЗНР) столбцы будут представлять все порожденные подграфы или остовные подграс^ы с заданными Свойствами, а строки матриц будут представлять вершины или ребра графа. В гл. 4,

например, задача о нахождении хроматического числа графа G рассматривается как ЗНП, в которой строки матрицы Т соответствуют вершинам графа G, а столбцы - максимальным независимым множествам вершин графа G (т. е. максимальным вполне несвязным подграфам графа G).

Другие задачи связаны с изучением покрытий ребер графа или его остовными подграфами с диаметром, не превосходящим А [13], или звездами ( звездными деревьями графа), или простыми цепями и циклами [16, 42].

6. Задачи

1. Перечислить все максимальные независимые множества графа G, показанного на рис. 3.6, и, следовательно, найти число независимости a[G].

2. Используя метод из разд. 2.3.2, составить список всех максимальных независимых множеств графа, приведенного на рис. 3.7. (Обратить внимание на симметрию графа.)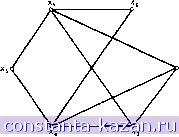

Рис. 3.6.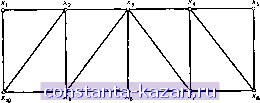

Рис. 3.7.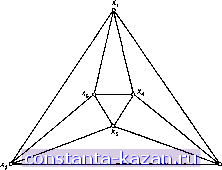

Рис. 3.8.

3. Показать, что для данного графа G = {X, Г) независимое множество Аа X является наибольшим тогда и только тогда, когда для произвольного независимого множества Ва X - А справедливо неравенство:

B\T{B)[jA\

(см. [63]).

4. Показать, что в полном неориентированном графе Кп каждое ребро принадлежит ровно п - 2 треугольникам (т. е. циклам длины 3).

5. Легко показать, что утверждение, обратное приведенному выше в задаче 4, неверно, т. е. если каждое ребро в графе G содержится ровно в га - 2 треугольниках, то граф G не обязательно совпадает с К„. (На рис. 3.8 приведен граф, в котором каждое ребро принадлежит только двум треугольникам, но граф отличен от К^.) Но приведенное в задаче 4 утверждение можно использовать для нахождения верхней оценки кликового числа графа G, т. е. такого наибольшего числа г, что в графе G содержится подграф Кг- Соответствующая оценка кликового числа графа G получается следующим образом:

(i) Начать со значения г, равного нижней границе кликового числа рассматриваемого графа.

(ii) Удалить те ребра, которые не содержатся хотя бы в г - 2 треугольниках.

(iii) Повторять (ii) для г = г--1, г--2ит. д., до тех пор, пока не останется ребер меньше, чем г (г - 1)/2. Текущее зна-