Шаг 1. Положить г = 1. Найти множества вершин S\. [G], 7 = 1, . . ., qr, максимальных г-подграфов графа G. (Считаем, что имеется Qr таких множеств.) Пусть Q = {S. [G] / = 1, . , ., g,}. Положить / = 1.

Шаг 2. Найти максимальное независимое множество {G] графа G = {X - S{ [G]). Если такое множество существует, то перейти к шагу 3. Если все такие множества уже найдены, то перейти к шагу 6.

Шаг 3. Вычислить S = S{ [G] \j [G].

Шаг 4. Если S - X, то остановиться. Число г -Ь 1 есть хроматическое число графа G. Подмножества, включенные в множество S, дают требуемую раскраску. (Эти подмножества накапливаются по мере их введения и хранятся отдельно с соответствующими отметками (маркерами)). Если S Ф= X, то перейти к шагу 5.

Шаг 5. (i) Если S S для некоторого S Q, то перейти к шагу 2.

(ii) Если S S для некоторых S g Q, то положить Q = = Q - {S} по всем таким S из Q. Положить Q = Q {] {S} и перейти к шагу 2.

(iii) Если не выполняется ни одно из условий (i) и (ii), указанных выше, то положить Q = Q [j {S} и перейти к шагу 2.

Шаг 6. Если / < Qr, то положить j = / -Ь 1 и перейти к шагу 2.

Если / = Qr, то положить j = I, г = г + I, Qj. - числу множе-жеств ъ Q ж перейти к шагу 2.

Если работу алгоритма не завершать при первом выполнении условия 5 = X на шаге 4, то алгоритмический процесс будет продолжаться до получения раскраски в г + 1 цветов, если такая раскраска существует. Следует отметить, однако, что описанный алгоритм не дает полного перечисления всех возможных раскрасок в г -f- 1 цветов, а только порождает оптимальные независимые раскраски. Такие раскраски могут оказаться только небольшой частью всех возможных раскрасок ъ г + I цветов.

3.1.4. Пример. Рассмотрим семивершинный граф G, изо браженный на рис. 4.3.

Шаг 1. Множествами вершин максимальных 1-подграфов являются: S\ [G] = {1, 4, 6}; S\ [G] = (2, 3, 5}; S\ [G] = = {2, 5, 7}; S\ [G] = {2, 6}. Следовательно, gi = 4 и Q = = {S\{G], S\{G], S\{G], S\[G]}.

Применяем (необходимое число раз) шаги 2-5 алгоритма:

Для S\{G]

Шаг 2. G - (Z - S\ [G]) = ({2, 3, 5, 7}); m ={2, 3, 5}.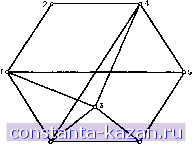

Рис. 4.3. Граф из примера 3.1.4.

Шаг 3.3 = {1, 4, 6 f 2, 3, 5}. Шаг 5. Q = [{1, 4, 6 f 2, 3, 5)]. Шаг 2. Si [СЧ = {2, 5, 7}. Шаг 3. S = {1, 4, 6 f 2, 5, 7).

Шаг 5. Q = [{1, 4, 6 2, 3, 5}, {1, 4, 6 f 2, 5, 7}]. Для S\ [G]

Шаг 2. G2 = ({1, 4, 6, 7}); S = {1, 4, 6). Шаг 5. = {2, 3, 5 f 1, 4, 6}, исключено в соответствии с шагом 5 (i).

Шаг 2. S [G = {!}. Шаг 3. S = {2, 3, 5 f 7).

*Шаг 5. Q = [{1, 4, 6 f 2, 3, 5), {1, 4, 6 f 2, 5, 7}, {2, 3, 5 f 7}].. Для SIG]

Шаг 2. G = ({1, 3, 4, 6}); S [G ] = {1, 4, 6). Шаг 5. = {2, 5, 7 f 1, 4, 6), исключено в соответствии с шагом 5(i).

Шаг 2. S [G ] = {3}.

Шаг 3. S = {2, 5, 7 f 3), исключено в соответствии с шагом 5(i).

Для St [G]

Шаг 2. G4 = {1, 3, 4, 5, 7}, S [G*] = {1, 4). Шаг 3. S = {2, 6 f 1, 4}, исключено в соответствии с шагом 5(i).

Шаг 2. Si [G] = {3, 5}.

Шаг 3. S = [2, 6 f 3, 5}, исключено в соответствии с шагом 5(i).

Шаг 2. Si {G] = {5, 7}.

Шаг 3. S = {2, 6 5, 7}, исключено в соответствии с шагом 5 (i).

Таким образом, в конце первой итерации, использующей шаги 2-5 алгоритма, получается семейство Q множеств S{ [G], соответствующее максимальным 2-подграфам и показанное на шаге, отмеченном звездочкой. Следует обратить внимание на то, что 5 из восьми полученных множеств исключены в результате применения первого правила из шага 5 алгоритма.

Действуя аналогичным образом дальше, можно построить максимальные 3-подграфы и т. д. В действительности уже следующее порожденное множество [G\ = {1, 4, 6 2, 5, 3 f 7} будет удовлетворять условию SI [G] = Z на шаге 4. Следовательно, хроматическое число графа равно 3 и оптимальная раскраска задается следующи.м разбиением (множества X) : {1, 4, 6}, {2, 5, 3}, {7}. Если применять алгоритм дальше, то будет получена еще одна возможная раскраска:

6[С]={1,4,62,5,73} = Х.

Все другие множества S [G] либо содержатся в двух предшествующих множествах, либо не содержат все вершины из X.

Заметим, что такие раскраски, как {5, 3}, {1, 4, 6}, {2, 7}, хотя и возможны, но не являются оптимальными независимыми и не порождаются описанным выше алгоритмом.

3.2. Формулировка задачи о раскраске на языке 0-1-программирования

Пусть q - какая-нибудь верхняя оценка хроматического числа графа G. Эта верхняя оценка может быть одной из оценок, данных в разд. 2 этой главы, или может быть равна числу цветов, получающемуся в одном из тех эвристических методов решения задачи о раскраске, которые подробно будут описаны позже.

Пусть 3 = lij] - матрица раскраски графа (задающая некоторую конкретную раскраску ) вершин графа), так что

1, если вершина Xi окрашена в цвет /, в противном случае.

) Здесь не предполагается, что смежные вершины должны быть окрашены в разные цвета. Если же это условие выполняется, то раскраска называется допустимой.- Прим. ред.