5.2. Составление графиков осмотра (проверки) [25] [2 4]

В задачах теории расписаний ) осмотры представляются в виде временных интервалов. Каждому осмотру можно сопоставить верпшну некоторого графа, причем две любые вершины графа будут соединены ребром лишь тогда, когда соответствую-щав им осмотры нельзя осун];ествлять одновременно. Требуется составить такой график осмотра, который связан с наименьшими временными затратами (с учетом приведенных выше ограничений на совместимость осмотров). Эта задача эквивалентна задаче о раскраске вершин графа с использованием наименьшего числа цветов. Хроматическое число графа как раз и соответствует осмотру, требуюгчему наименьших временных затрат.

Если число осмотров, которые можно осуш;ествлять в одно и то же время, ограничено (например, из-за размеров помен];е-ния), то приходим к задаче типа (i) из разд. 5.1, и Q в этом случае является числом помегчений, где происходит осмотр.

5.3. Распределение ресурсов

Пусть для выполнения каких-то п работ надо распределить т имеюгчихся в наличии ресурсов. Считаем, что каждая из работ выполняется за некоторый (одинаковый для всех работ) промежуток времени и что для выполнения i-й работы требуется подмножество ресурсов Si. Построим граф G: каждой работе соответствует определенная верхпина графа, а ребро (х,-, Xj) сун];ествует в графе тогда и только тогда, когда для выполнения i-й и /-й работ требуется хотя бы один обилий ресурс, т. е. когда Si (] f\ Sj ф 0. Это означает, что1-я и j-я работы не могут выполняться одновременно. Раскраска графа G определяет тогда некоторое распределение ресурсов (но выполняемым работам), причем такое, что работы, соответствуюгчие вершинам одного цвета, выполняются одновременно. Наилучшее использование ресурсов (т. е. выполнение всех п работ за наименьшее время) достигается при оптимальной раскраске вершин графа G.

6. Задачи

1. Для графа, показанного на рис. 4.5, вычислить верхние и нижние оценки хроматического числа, используя результаты, приведенные в разд. 2.1 и 2.2.

1) В отечественной литературе применяется также термин задача календарного планирования .- Прим. ред.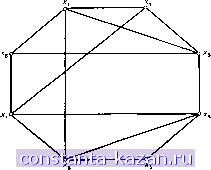

Рис. 4.5.

2. Используя алгоритмы из разд. 3.1 и 3.4, найти для графа на рис. 4.5 хроматическое число и соответствующую этому числу раскраску. Сравнить вычислительную сложность этих алгоритмов (для данного графа).

3. Для графа, изображенного на рис. 3.6 из гл. 3, найти хроматическое число и соответствующую раскраску, формулируя задачу о раскраске как ЗНП.

4. Применить последовательные методы, основанные на рассмотрении степеней di, dj и df, для получения оптимальной -раскраски графа, приведенного на рис. 4.5.

5. Доказать, что хроматическое число каждого га-вершинного дерева (га2) равно 2.

6. Показать, что граф 2-хроматический тогда и только тогда когда все его циклы имеют четные длины.

7. В ПЛОСКОСТИ проведено конечное число прямых линий; они разбили ее на конечное число областей. Показать, что достаточно 2 цвета для такой раскраски всех этих областей, когда любые две смежные области окрашиваются в разные цвета.

8. Граф на рис. 4.6 представляет схему электрических соединений; вершины соответствуют клеммам, ребра - прямым металлическим полоскам проводников. Для физически осуществимых соединений проводники не должны пересекать друг друга, поэтому необходимо распределить ребра по нескольким параллельным

платам, в каждой из которых проводники не пересекались бы. {Клеммы доступны на всех платах.)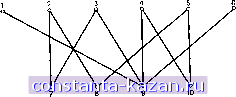

- Проводники

Клеммы

Рис. 4.6.

Определить наименьшее число плат, необходимых для реализации этих соединений (см. [14] и [7]).

9. На трех предприятиях выпускается одиннадцать видов изделий А, В, . . ., К, причем каждый вид производится только на одном из трех предприятий. Процент общих деталей и материалов, используемых в производстве каждых двух видов изделий, приводится в следующей матрице:

Желательно, чтобы на одном предприятии выпускались изделия с большим процентом общих деталей и материалов, потребляемых при их производстве. Требуется так распределить производство изделий на предприятиях, чтобы минимум общих поставок для производства двух любых видов изделий на одном и том же предприятии был как можно больше.