графа G, определяются следующим образом:

So{y) = may.\Vid{y,Xi)], (5.6)

а для S( {у) соответствующее выражение получается из соотношения (5.2).

Точка !/*, для которой

s,{y*o)= min К(г/)1, (5.7)

у из G

называется абсолютным внешним центром графа; и аналогично определяется у* - абсолютный внутренний центр.

Число внешнего разделения абсолютного внешнего центра называется абсолютным внешним радиусом: Го = Sq (у*), и число внутреннего разделения абсолютного внутреннего центра называется абсолютным внутренним радиусом: rt = St{y*).

Пример. Рассмотрим неориентированный граф G, показанный на рис. 5.3, где все веса вершин и длины ребер равны единице.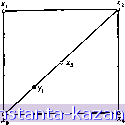

Рис. 5.3. Абсолютный центр.

Поскольку граф неориентированный, то числа внешних и внутренних разделений одинаковые (для одной и той же вершины). Матрица расстояний графа имеет вид

D{G) = хз

Нетрудно видеть, что центром является каждая вершина и что радиус равен 2.

Если теперь выбрать точку на ребре (хд, х^) так, что

1 / 1 \

( 51 Ui) = f ( следовательно, I {у^, Хд) = у j , то расстояния

от этой точки до вершин графа даются таблицей

Значит, наибольшее число разделения равно 1у . Таким образом,

точка Ух более центральна , чем любая из вершин графа G. В действительности точка Ух является абсолютным центром графа G - так же, как и все точки, расположенные в середине ребер {хх, х^), (xj, Xs), {xs, Xi), {Xi, x) и (xg, Xx). Ни одна из вершин графа не является абсолютным центром. Таким образом, в общем случае может быть один или больше абсолютных центров, которые располагаются или в вершинах, или на дугах графа.

5. Алгоритмы нахождения абсолютных центров

Центры и радиусы графа можно найти непосредственно из матрицы взвешенных расстояний, как было показано в разд. 2 и 3. Приведем два метода нахождения абсолютного центра графа и проиллюстрируем эти методы на примере.

5.1. Метод Хакими [7j

Этот метод очень прост и для неориентированного графа состоит в следующем (для ориентированного графа метод остается таким же, надо только каждое неориентированное понятие заменить его ориентированным двойником ).

(1) Для каждого ребра графа найти точки (или точку) у* на uft, которые имеют наименьшее число разделения.

(ii) Из всех точек у* {к = \, 2, . . ., т) в качестве абсолютного центра графа G выбрать точку с наименьшим числом разделения.

Первый шаг метода осуществляется следующим образом.

Остаток графа G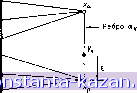

Рис. 5.4.

Возьмем ребро графа G (см. рис. 5.4). Имеем (из соотношения (5.6)):

S (1/0 = max [Vid {yk,Xi)] =

= max [17; min {/ (y, x) + d (x, Xt), I {y, Xa) + d{Xa, Xi)}], (5.8)

поскольку расстояние d (уи, Xi) равно либо длине маршрута, проходящего через вершину Ха, либо длине маршрута, проходящего через Xq, I (i/ft, Ха) и / (j/, а:в) являются длинами соответствующих частей ребра а^.

Пусть I (г/й, х^) = . Поскольку I {уи, а: ) = с„в -Z {уи, х^) = = c g - I, то соотношение (5.8) примет вид

S [уи) = max min {ь\ {l-\-d {х^, Xi)}, Vi {Саэ + d{Xa.,Xi) - I)]. (5.9)

Для фиксированной вершины Xi и при каждом значении I (0c g) можно найти наименьшие значения выражений, заключенных в соотношении (5.9) в квадратные скобки. Для этого выпишем отдельно два указанных выражения:

Ti = Vi{l + d{x,x{)},

T\ = Vi{c, + d{Xa,Xi)-l}

и, рассматривая их относительно , строим нижнюю огибающую для соответствующих им прямых линий ).

Повторяя эту процедуру для всех вершин Xi £ X, мы построим на одном и том же чертеже все остальные нижние огибающие . Далее вычертим верхнюю огибающую для всех ранее полученных нижних огибающих , которая (в силу соотношения (5.9)) дает числа разделения s (у^) для всех значений параметра , т. е.

1) В действительности эта огибающая представляет собой ломаную линию, состоящую из двух нижних лучей (от точки пересечения) рассматриваемых прямых линий.- Прим. ред.