для всех точек ребра а^. Построенная огибающая (она составлена из линейных кусков) может иметь несколько минимумов. Точка соответствующая наименьшему из этих минимумов, является (в силу соотношения (5.7)) абсолютным центром у*, отвечающим дополнительному ограничению: он должен лежать на ребре о^. Абсолютным центром графа будет такая точка у*, которой соответствует наименьший из минимумов, определяющих указанные выше абсолютные центры на ребрах (/с = 1, 2, ...

5.2. Размещение аварийных служб (общий случай)

Рассмотрим еще раз задачу об обслуживании нескольких районов каким-либо одним пунктом обслуживания (одной больницей, или пожарным депо, или полицейским участком). Если опущено ограничение, состоящее в том, что пункт обслуживания должен размещаться в каком-то из жилых районов (см. разд. 3.1), то оптимальным размещением пункта обслуживания будет его размещение в любом абсолютном центре соответствующего графа.

Рассмотрим, например, неориентированный граф, приведенный на рис. 5.5. Пусть вершины графа соответствуют жилым районам, а длина ребра (х^, Xj) равна времени (в минутах), необходимому для проезда из района Xi в район Xj. Предположим, что вершины графа имеют единичные веса и матрица расстояний (времен) такова:

Очевидно, что центром графа является либо вершина Xi, либо JTs и что радиус графа равен 8.

Сначала возьмем ребро Ui (рис. 5.5), и пусть расстояние измеряется от вершины Xg до вершины Xi.

Выражения Г; и Т1 из соотношений (5.10) (для i = 1, 2, ... . . ., 5) имеют в нашем случае такой вид: Ti = l + d{xs, Xi)=E-f 8, r; = C3.i + d(a;i,a;i)-g = 8-g,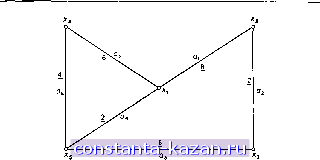

Рис. 5.5. Граф из примера разд. 5.2.

аналогично

7-2 = +2,

T, = l + i2, 7. = Е + 8,

г; = 1б-£, r = io-L

Графики этих функций изображены на рис. 5.6а, для 0- £8. Имеются два локальных абсолютных центра у* на расстоянии 6 и 8 минут ОТ Xg. Число разделения этих двух центров равно 8 минутам.

Аналогично строятся графики для ребер а. а^, . . ., см. рис. 5.6 б-е. Абсолютный центр (г/*) этого графа есть такой локальный центр, который имеет наименьшее число разделения. Он, как легко видеть, находится на ребре (рис. 5.6в) в двух минутах от х^. Абсолютный радиус г (соответствующий у*), как видно из рис. 5.6, равен 6.

5.3. Модифицированный метод Хакими

В описанном выше методе Хакими поиск локального центра осуществляется вдоль всего ребра графа G. Если в графе много ребер, то время вычисления, требуемое для поиска, может оказаться чрезвычайно большим. Рассматриваемая в данном разделе модификация метода Хакими состоит в вычислении верхних и нижних оценок абсолютных локальных радиусов, соответствующих локальным центрам ребер, и в использовании полученных оценок для уменьшения числа ребер, участвующих в поиске.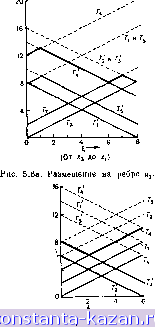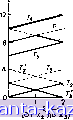

Рис. 5.66. Размещение на ребре Oj.

/Значение , абсолютного \ радиуса )

fПоложение \ 1 ,пт V пп у \ глобального)-1° центра

Рис. 5.6в. Размещение на ребре og. Рис. 5.6г. Размещение на ребре а^.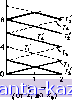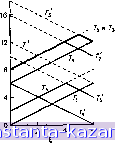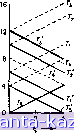

° (ОТ Х4 до Хб

Рис. 5.6д. Размещение на ребре Oj. Рис. 5.бе. Размещение на ребре ag.