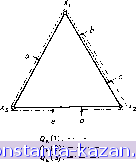Рис. 5.7. Области, образованные при к - 3.

Область 1. Точка а (единственная точка, из которой в пределах расстояния, равного 3, достижимы вершины Xj и Хз).

Область 2. Отрезок ребра (xi, х^) от b до с. (Из любой точки этой области достижимы вершины Xj и Xg.)

Область 3. Отрезки {а, Xi) и (xi, соответствующих ребер (из точек этой области достижима только вершина Xt).

Область 4. Отрезки (а, Хд) и (xg, е) соответствующих ребер (из каждой точки этой области достижима только Хз).

Область 5. Отрезки (с, и (х^, d) (из точек этой области достижима только Хз).

Область 6. Отрезок ребра (хг, Xg) от е до d (из точек этой области не достижима никакая вершина).

В общем случае все области Ф% можно следующим образом построить из достижимых множеств <х-

Области, из которых не достижимы никакие вершины ), описываются соотношением

Ф}. (0) = (у U на G} - и Q% (Xi), (5.22)

где второй член исключает все области графа G, из которых можно-достигнуть ) хотя бы одну вершину х,-.

Области, из которых можно достигнуть ) ровно t вершин Xi,Xi, . . ., Xi (для любого < = !,..., ), определяются сле-

1) Всюду в этих рассмотрениях достижимость берется в пределах заданного расстояния fi; .- Прим. ред.

дующим выражением:

Фя(.Г;.,Х , ...,Xi )= П QxiXi)-* 9=1.....t

-{[ n QUO](][ и )]}, (5.23)

q=i, ..., t q=t+i, ...,n 1

где второй член исключает такие области, из которых достижимы вершины Xi, Xi, . . ., XiH еще хотя бы одна из оставшихся вершин графа.

С первого взгляда кажется, что число областей из соотношения (5.23) может быть очень велико. Однако на практике пересечения множеств, входящие в выражение (5.23), становятся пустыми уже для небольших значений t. Это приводит к вполне обозримому множеству областей. Эффективные (с вычислительной точки зрения) методы построения областей, а также дальнейшего уменьшения числа необходимых областей приводятся в настоящем разделе несколько позже.

8.1. Описание алгоритма

Алгоритм построения абсолютного р-центра графа G ~ {X, А) при заданном р выглядит следующим образом.

Шаг 1. Положить А = 0.

Шаг 2. Увеличить К на небольшую величину АХ,. Шаг 3. Построить множества Qx (xt) для всех g Х„ и найти области Ф^.

Шаг 4. Образовать двудольный граф G - {X [] X, А'), где X-множество вершин, каждая из которых соответствует некоторой области Ф;, и А' - множество дуг, такое, что дуга между областью-вершиной и вершиной Xi существует тогда и только тогда, когда Xi может быть достигнута из этой области.

Шаг 5. Найти наименьшее доминирующее множество графа G (см. гл. 3).

Шаг 6. Если число областей в приведенном выше множестве больше, чем р, то вернуться к шагу 2; в противном случае остановиться. Области этого множества образуют абсолютный /?-центр исходного графа G.

Следует отметить (см. гл. 3), что число областей в наименьшем доминирующем множестве представляет (по определению) наименьшее число точек в G, из которых достигаются все вершины графа в пределах расстояния проникновения Я, используемого в данной итерации. Надо также отметить, что в процессе построения абсолютного /7-центра по указанному выше алгоритму можно заодно получить абсолютные {п - 1)-, {п - 2)- и т. д. центры. Таким образом, если в конце некоторой итерации (продолжающейся с шага 2 до шага 6) число областей в наименьшем доминирующем

множестве уменьшается с некоторого уровня Z до Z - 1, то области ЭТОГО нового множества образуют абсолютный (Z - 1)-центр, а величина Я, взятая для этой итерации, будет абсолютным (Z-1)-радиусом , т. е. она является критическим значением Л - при меньших значениях Л не существуют (Z - 1)-центры, из которых в пределах взвешенного расстояния % достижима каждая вершина графа.

Если нужно найти такое наименьшее значение р, что каждая вершина достижима из некоторого центра в пределах заданного критического расстояния (задача (Ь) из разд. 7), то шаги с 3 по б в приведенном выше алгоритме следует выполнять при Я, равном этому критическому значению. Соответствующее число областей в наименьшем доминирующем множестве является тогда требуемым значением для р, и области этого множества образуют искомый jD-центр.

8.2. Вычислительные аспекты

Предположим, что Л зафиксировано и вычислены расстояния б; = Я/у;. Любое ребро графа либо достижимо целиком, либо частично, либо совсем не достижимо из вершины Х; в пределах расстояния б;. Если достижима только часть ребра (от какого-либо конца ребра до некоторой предельной точки на нем), то над предельной точкой ставится метка . Эти метки содержат всю информацию, необходимую для описания множеств {х{). Таким образом, Qx (х;) состоит из точек всех ребер (или частей ребер), принадлежащих кратчайшим маршрутам между метками и вершиной Xi.

После размещения всех меток (для всех вершин) каждое ребро будет разделено на ряд участков; каждый участок характеризуется теми вершинами, которые из него ) могут быть достигнуты. Таким образом, любой участок можно описать бинарным (единица-нуль) вектором {/ь /а, . . ., / } длины п, в котором = 1, если вершина х^ достижима из этого участка, и = О в противном случае.

Совокупность всех участков с одинаковым бинарным вектором образует область, и, следовательно, области Ф;, задаваемые соотношениями (5.23), могут быть построены с помощью таких меток. Поскольку область достижима только из тех вершин, для которых = 1 (в бинарном векторном представлении этой области), и не из каких других, то в дальнейшем эти бинарные векторы мы будем называть строгими пересечениями (SI).

Представление области бинарным вектором не содержит никакой информации о месте ее расположения на графе. Однако такое представление выгодно с вычислительной точки зрения: оно не

) То есть из точек этого участка.- Прим. ред.