{Za, Xg) В первоначальном дереве ориентировано от Ха к Xg) пометки в дереве Ti можно оставить прежними, а пометки в дереве должны быть изменены. Если же ра = Xg (т. е. ребро {ха, Xg) ориентировано от Xg к Ха), то можно не менять пометки в дереве Гг, но нужно изменить пометки в Ti. Предполагая, что пометки меняются в дереве Т^, покажем, как надо восстанавливать корень в этом дереве.

1. Положить 5 = {xg} и pg = О (xg будет корнем дерева Т^).

2. Найти все вершины xj с Pj S и изменить их корневые пометки на rj = Xg. Если таких вершин нет, остановиться.

3. Шаг обновления: S = S \j {Xj \ pj 6 S}; вернуться к шагу 2.

Следует отметить, что ни у одной вершины, кроме нового корня Xg, пометки предшествования менять не нужно. Заметим также, что число описанных выше шагов 2 и 3, которое необходимо для восстановления корня, равно длине самой длинной цепи в Т^, исходящей из вершины Xg.

2.2.2. Описание алгоритма. Возьмем произвольную вершину X* графа G. Пусть ее степень равна d*. Перенумеруем ребра, инцидентные этой вершине: а^, а^, . . ., а^*. Затем перенумеруем остальные ребра графа G: ad*+i, dm- При порождении деревьев ребра будут перебираться в соответствии с введенной нумерацией.

Шаг 1. Приписать вершинам пометки: (г р^), где = xi и == О, Vxj 6 X. Положить к = i.

Шаг 2. Выбрать для исследования некоторое ребро. Например, ah = {Xi, Xj). Если к^т, где т - число ребер графа, то перейти к 2 (i). При к = т i, т. е. если неисследованных ребер нет, перейти к шагу 5.

(i) Если Гг = rj, то это означает, что вершины х, и Xj принадлежат одному и тому же поддереву и добавление ребра а^ приведет к появлению цикла. Отбросить ребро а^, т. е. положить к = к + -Ь 1 и вернуться к шагу 2,

(ii) Если Гг Ф rj, то ребро а^ можно добавить к ребрам построенных поддеревьев. Перейти к шагу 3.

Шаг 3. Срастить два поддерева, у которых вершины имеют корневые пометки и rj, применив для этого метод, описанный выше в пункте Б.

Шаг 4. Отобрав п - 1 ребер, мы получаем некоторое дерево. Запомнить это дерево и перейти к шагу 5. Если отобрано меньше чем п - 1 ребер, то положить к = к + I и вернуться к шагу 2.

Шаг 5. (Возвращение.) Удалить ребро, добавленное последним. Предположим, что таким ребром является aj. Если aj -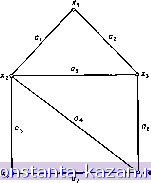

Рис. 7.7. Граф из при.мера 2.3.

единственное оставшееся для добавления ребро, I = d*, то остановиться. Все остовные деревья, таким образом, построены. (При любом дальнейшем ветвлении дерева решений вершина х* останется пзолированной.)

В противном случае надо обновить пометки, действуя так, как указано в пункте В, положить /с = Z + 1 и возвратиться к шагу 2.

2.3. Пример

Нам нужно построить все остовные деревья графа, изображенного на рнс. 7.7. Выберем в качестве х* вершину Xj; имеем d* = = 2. Обозначим ребро {Xi, х^) через aj, а ребро (xj, х^) через а^. Остальные ребра перенумеруем, например так, как показано на рис. 7.7 (ребра з, 4, . . ., a).

На рис. 7.8 изображено соответствующее дерево решений (оно порождено в процессе работы алгоритма, приведенного в разд. 2.2.2). Если взять ребра, указанные в кружочках какой-либо цепи, выходящей из верхнего узла этого дерева и оканчивающейся в самом нижнем узле, то из них можно построить некоторый остов данного графа. Эти остовы перенумерованы числами от 1 до 21 и приведены на рис. 7.9.

Легко проверить, что у графа, изображенного на рис. 7.7, действительно 21 остов. Это можно установить с помощью теоремы 1 из разд. 2. Матрица инциденций В данного графа имеет следующий вид (считаем, что каждое ребро ориентировано от его конце-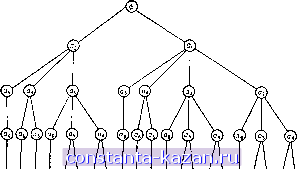

©О©©©©©©©©©©©©©

21 20 19 18 17 16 15 14 13 12 II 10 9 8 7 6 5 4 3 2 1 Рис. 7.8. Полное дерево поиска из примера 2.3.

о Ъ 6 6 о о о--о о 1 2 3 4 5 6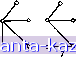

6 6 6--о о 6 6

/, А

о о 6--о о о 6

8 9 10 11 12 13 14

\ А А А А А А

15 16 17 18 19 20 21

Рис. 7.9. Все остовы графа с рис. 7.7.