(Х 15)

(-<7. Э)

(0.=°) (Х7,13)

Рис. 7.13а. Частично сформированное дерево с пометками на вершинах, не принадлежащих 2*. ---Надо добавить следующее ребро.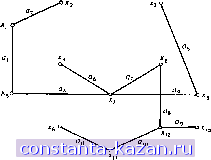

Рис. 7.136. SST графа на рис. 7.12.

4. Задача Штейнера

В предыдущем разделе в задаче определения SST, т. е. наикратчайшего дерева графа G = (Z, Г), ребрами покрывались все вершины множества X. С зтой задачей тесно связана задача, известная как тадача Штейнера на графах) [27, 18], но последняя значительно труднее.

В этой задаче требуется найти наикратчайшее дерево Т, которое стягивает ( покрывает ) заданное подмножество Рс X вер-

ШИН графа G. Другие вершины, нринадлежаш;ие X - Р, могут либо стягиваться деревом Т, либо нет, в зависимости от требования минимизации длины дерева Т. Таким образом, задача Штейнера на графе эквивалентна нахождению наикратчайшего остовного дерева произвольного подграфа G = {X, Г) графа G при условии Р = Е Z Z.

Евклидова задача Штейнера впервые была поставлена как геометрическая задача [13, 14, 44, 24], в которой нужно множество точек Р на евклидовой плоскости соединить линиями так, чтобы сумма длин отрезков была минимальна. Если не допускаются пересечения любых двух линий в точках вне заданного множества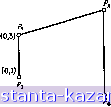

(4,4)

Рис. 7.14а. Кратчайшее остовное дерево. Длина = 10,123.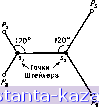

Рис. 7.146. Кратчайшее дерево Штейнера. Длина 9,196.

Р, то задача сводится к одной из задач определения SST эквивалентного графа на I вершинах с матрицей весов, вычисленных как евклидово расстояние между точками множества Р. Если допускается на плоскости введение дополнительных искусственных вершин (называемых точками Штейнера), то длину SST на множестве точек Р' Р можно уменьшить соответствуюш;им подбором точек. Например, для четырех точек, показанных на рис. 7.14а, SST имеет длину, большую, чем SST графа, получаемого после добавления двух новых точек % и Sg, расположенных между исходными точками (см. рис. 7.146). Таким образом, для решения задачи Штейнера можно добавить в любых местах плоскости столько точек Штейнера, сколько необходимо для построения наикратчайшего дерева, стягиваюш;его множество из Р точек. Получаюш;ееся наикратчайшее дерево называют наикратчайшим деревом Штейнера.

Задача Штейнера на евклидовой плоскости достаточно хорошо изучена [44, 24, 11, 12], и известно большое число свойств наикратчайшего дерева Штейнера. Наиболее важными свойствами являются следуюш;ие [24, 11]:

(i) Точка Штейнера имеет степень d {si) = 3. Это можно легко показать с помощью геометрического построения, поскольку угол между ребрами, инцидентными точке Штейнера Sj, должен быть равен 120° и точно три ребра инцидентны любой точке Штейнера Si. Следовательно, эта точка является центром (центром Штейнера) воображаемого треугольника, вершинами которого

Рис. 7.15а. Кратчайшее остовное дерево. Длина = 18.

! Точки Штейнера

Рис. 7.156. Кратчайшее дерево Штейнера. Длина = 15.

являются три другие точки дерева, с которыми она связана с помощью наикратчайшего дерева Штейнера.

Некоторые точки, являющиеся вершинами такого треугольника, могут оказаться другими точками Штейнера. Например, на рис. 7.146 точка Штейнера является центром воображаемого треугольника с вершинами Рз, и s.

(ii) Для вершины Pt Р степень d (pj) 3. Если d (pi) =3, то угол между любыми двумя ребрами, инцидентными pi, должен быть равен 120°. Если d (pi) = 2, то угол между двумя ребрами, инцидентными р,-, должен быть больше или равен 120°.

(iii) Число точек Штейнера в наикратчайшем дереве Штейнера равно к, О к п - 2, где п = \ Р \. Доказательство упомянутых выше свойств можно найти в 124].

Несмотря на то внимание, которое уделялось евклидовой задаче Штейнера, при помощи существуюпих алгоритмов [44, 11] решение возможно только для небольших но размеру задач (не более 10 точек в Р) и, следовательно, можно считать евклидову