Присвоение начальных значений

Шаг 1. Положить Z (s) = 0 и считать эту пометку постоянной. Положить I{xi) - оо для всех Xism считать эти пометки временными. Положить р = S.

Обновление пометок

Шаг 2. Для всех Xj £ Г (р), пометки которых временные, изменить пометки в соответствии со следующим выражением:

I {Xi) min [1 {Xi), 1{р) + с {р, Xi)]. (8.1)

Превращение пометки в постоянную

Шаг 3. Среди всех вершин с временными пометками найти такую, для которой Z(x*) = min [I (Xi)].

Шаг 4. Считать хгометку вершины х* постоянной и положить

Р - i-

Шаг 5. (i) {Если надо найти лишь путь от s к t.) Если p = t, то I (р) является длиной кратчайшего пути. Останов.

Если р Ф t, перейти к шагу 2.

(ii) {Если требуется найти пути от s ко всем остальным вершинам.)

Если все вершины отмечены как постоянные, то эти пометки дают длины кратчайших путей. Останов.

Если некоторые пометки являются временными, перейти к шагу 2.

Доказательство того, что вышеприведенный алгоритм действительно дает кратчайшие пути, чрезвычайно простое, дадим набросок этого доказательства.

Допустим, что на некотором этапе постоянные пометки дают длины кратчайших путей. Пусть - множество вершин с этими пометками, а 2 - множество вершин с временными пометками. В конце шага 2 каждой итерации временная пометка I {xi дает кратчайший путь от s к Xj, проходящий полностью по вершинам множества i. (Так как при каждой итерации в множество включается только одна вершина, то обновление пометки I (х;) требует только одного сравнения на шаге 2.)

Пусть кратчайший путь от s к х* не проходит целиком по и содержит по крайней мере одну вершину из S., и пусть Xj 6 S. - первая такая вершина в этом пути. Так как по предположению Cij неотрицательны, то часть пути от х; к х* должна иметь неотрицательный вес Д и I {х}) < I (х*) - Д < Д(х*). Это, однако, противоречит утверждению, что I {xf) - наименьшая временная пометка, и, следовательно, кратчайший путь к х* проходит полностью по вершинам множества S-, и поэтому I (х*) является его длиной.

Заметим, что нет никакой связи между понятием базы и понятием базы графа, введенным ранее в гл. 2.

Так как вначале множество Si равно (s) и при каждой итерации к Si добавляется xf, то предположение, что I (Xi) равно длине кратчайшего пути Xi Si, выполняется при каждой итерации. Отсюда по индукции следует, что алгоритм дает оптимальный ответ.

Если требуется найти кратчайшие пути между s и всеми другими вершинами полного связного графа с п вершинами, то в процессе работы алгоритма выполняются п (п - 1)/2 операций сложения и сравнения на шаге 2 и еще п {п - 1)/2 операций сравнения на шаге 3. Кроме того, при осуществлении шагов 2 и 3 необходимо определить, какие вершины являются временными, а для этого нужно еще п {п - 1)/2 операций сравнения. Эти величины являются верхними границами для числа операций, необходимых при отыскании кратчайшего пути между заданными вершинами S VI t. Они действительно достигаются, если окажется, что вершина t будет последней вершиной, получившей постоянную пометку. (В [22] Джонсон предложил так называемый метод сортировки, позволяющий уменьшить число операций на шаге 3.)

Как только длины кратчайших путей от s будут найдены (они будут заключительными значениями пометок вершин), сами пути можно получить при помощи рекурсивной процедуры с использованием соотношения (8.2). Так как вершина х1 непосредственно предшествует вершине х; в кратчайшем пути от s к Xj, то для люб|ОЙ вершины Xi соответствующую вершину х[ можно найти как одну из оставшихся вершин, для которой

l(xl) + c(x:,Xi)l{Xi). (8.2)

Если кратчайший путь от s до любой вершины х; является единственным, то дуги (xl, Xi) этого кратчайшего пути образуют ориентированное дерево (см. предыдущую главу) с корнем s. Если существует несколько кратчайших путей от s к какой-либо другой вершине, то при некоторой фиксированной вершине xi соотношение (8.2) будет выполняться для более чем одной вершины Xi. В этом случае выбор может быть либо произвольным (если нужен какой-то один кратчайший путь между s и Xj), либо таким, что рассматриваются все дуги (xi, Xi), входящие в какой-либо из кратчайших путей, и при этом совокупность всех таких дуг образует не ориентированное дерево, а общий граф, называемый базой относительно s или кратко - s-базой ).

2.1.2. Пример. Рассмотрим граф, изображенный на рис. 8.1, где каждое неориентированное ребро рассматривается как пара противоположно ориентированных дуг равного веса. Матрица

весов Ci приведена ниже. Требуется найти все кратчайшие пути от вершины Xi ко всем остальным вершинам. Мы воспользуемся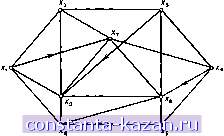

Рис. 8.1. Граф из примера 2.1.2.

алгоритмом Дейкстры. Постоянные пометки будем снабжать внаком -f, остальные пометки рассматриваются как временные.

Алгоритм работает так:

Шаз 1. I {xi) = О*, / (х,) = оо Vxi ф Xi, р =Xi.