1{х,)==Ъ*

Р = Хт

Шаг 5. Не все вершины имеют постоянные пометки, поэтому переходим к шагу 2. Пометки в начале следуюш,ей итерации показаны на рис. 8.2 (а).

Вторая итерация

Шаг 2. Г (р) = Г {x) = {х^, х^, х^, Хд) - все пометки временные. Из соотношения (8,1) имеем

Z(a;2) = min[10,3+ + 2] = 5,

аналогично I {х^) = 7, I {х^) = 17, 1(хд) = 12. Пометки изображены на рис, 8.2 (б).

Шаг 3. min [5, 7, 17, 6, 12, оо] = 5 соответствует х^.

ж, ж, X, X, X, х х,

Шаг 4. Х2 получает постоянную пометку 1{х2) = 5* , р=х^. Шаг 5. Перейти к шагу 2. Третья итерация

Шаг 2. Г (р) = Г {х^) = {хх, х^, Хт, Хд} - только вершины Xg и Ха имеют временные пометки; из соотношения (8.1) получаем

i(a;3) = min[oo, 5+-f 18] = 23

и аналогично

I (Хд) = 12.

Шаг 3. min [23, 7, 17, 6, 12, оо] = 6 соответствует Xg.

Р = Х8

Шаг 4. Xg получает постоянную пометку 1{х^=&* Шаг 5. Перейти к шагу 2,

Продолжая этот процесс, получим окончательную картину расстановки пометок, изображенную на рис. 8.2 (в). Для нахождения кратчайшего пути между вершиной х^, (например) и начальной вершиной Xg мы последовательно используем соотношение (8.2). Таким образом, полагая Хг=Х2, находим вершину Xg, непо-

Первая итерация

Шаг 2. Г (р) = Г {хх) = {х^, Хт, Xg, Хд} -все пометки временные. Возьмем сначала х^. Из (8.1) получаем

Z(a;2) = min[c , О*+ 10] = 10,

аналогично I {x) = 3, Z (xg) = 6, Z (хд) = 12.

Шаг 3. min (10, 3, 6, 12, оо) =3 соответствует x.

X, X, X, X, Xt,Xi,X X,

Шаг 4. х, получает постоянную пометку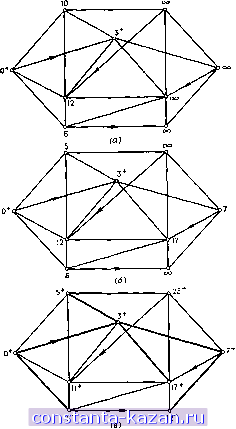

Рис. 8.2. (а) Пометки в конце 1-й итерации, (б) Пометки в конце шага 2 на 2-й итерации, (в) Окончательные пометки вершин и Xi-база.

средственно предшествующую в кратчайшем пути от х^ к х^: вершина х, должна удовлетворять соотношению

1{Х2) + С{Х' Х2) = 1{Х2) = 5.

Единственной такой вершиной является Хт. Далее, применяем второй раз соотношение (8.2), беря а;г=а;7; получаем вершину х' непосредственно предшествующую x в кратчайшем пути от Хх к Xg. Вершина х^ удовлетворяет соотношению

l{x)+c{x, x)==l{x) = 3.

Единственной такой вершиной является х^, и поэтому кратчайший путь от Xi к Х2 есть (х^, хт, х^. х^-база, дающая все кратчайшие пути от Xi, представляет собой дерево, изображенное жирными линиями на рис. 8.9, (в).

2.2. Случай общей матрицы весов

Только что описанный алгоритм Дейкстры применим лишь в том случае, когда cij > О для всех i и /. Однако если матрица С является матрицей стоимостей, то дуги, приносящие доход, должны иметь отрицательные стоимости . В этом случае для нахождения кратчайших путей между вершиной s и всеми другими вершинами можно воспользоваться описанной ниже процедурой. Этот метод также является итерационным и основан на пометках вершин, причем в конце к-ж итерации пометки равны длинам тех кратчайших путей (от s ко всем остальным вершинам), которые содержат не более /с + 1 дуг. В отличие от алгоритма Дейкстры никакая из пометок во время этого процесса не рассматривается как окончательная. Описываемый метод был первоначально предложен в середине 50-х годов Фордом [14], Муром [26] и Беллма-ном [2]. Перейдем к его описанию.

2.2.1. Алгоритм для общей матрицы весов

Пусть 1 {xi) - пометка вершины Xi в конце {к -f- 1)-й итерации.

Присвоение начальных знаний

Шаг 1. Положим 5 = Г (s), А; = 1, (s) = О, 1 [xi) = с (s, Xi) для всех Xj Г (s) и V- (xj) = оо для всех остальных х^.

Обновление пометок

Шаг 2. Для каждой вершины Xj 6 Г (s) (xj Ф s) изменить ее пометку следующим образом:

Z+i (Xj) = min [/ (Xj), min {Z (xy) +c (xy, xj)}], (8.3)