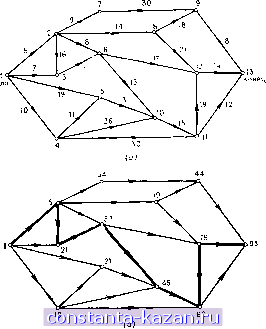Ihc. 8.5. (а) Граф из примера 6.1.1. (б) Окончательные пометки вершин и критический путь.

,И / - два последовательные этапа в самом длинном пути, то I (Xj) - I (xi) - Cij = 0.

6,1.1. Пример. Рассмотрим диаграмму ПЕРТ, изображенную на рис. 8.5 (а), где числа, стоящие у дуг, указывают продолжительность задержек в днях. Каков наименьший возможный срок Cij выполнения этого проекта? (Предполагается, что вершина 13 является конечной и ей соответствует нулевая продолжительность.) Вершины графа уже пронумерованы так, что дуга (Xj, Xj) существует лишь при xj > Xj. Применение выражения (8.7) к графу, изображенному на рис. 8.5 (а), приводит к расстановке

пометок, показанной на рис. 8.5 (б); критический путь изображен жирной линией. Длина этого пути и, следовательно, наименьший возможный срок выполнения проекта равен 93 дням.

Если один из этапов, принадлежапцих критическому пути, задерживается на D дней, то и весь проект задержится на тот же срок. С другой стороны, задержка, скажем, этапа 8 (не принадлежащего критическому пути) возможна на 79-19-21 = 39 дней, причем это не отразится на общем сроке реализации проекта. Лишь задержка на срок D > 39 дней повлияет на пометку вершины 12 (принадлежащую критическому пути).

Метод ПЕРТ описан в этой главе в терминах самого длинного пути в графе, вершины которого отвечают этапам выполнения проекта, а дуги - отношениям предшествования, причем вес Cij дуги (ж Xj) равен интервалу времени между началом этапа t и /. На практике диаграммы ПЕРТ истолковываются несколько иначе, а именно дуги представляют этапы, а вершины изображают абстрактные события , указывающие начала или окончания этапов. Хотя такое представление само по себе является неполным (так как при зтом отношения предшествования точно не описываются), указанный недостаток можно устранить, добавляя фиктивные этапы для точного описания отношений предшествования [34]. С другой стороны, такое представление имеет важное преимущество перед первоначальным, поскольку приводит на практике к более простым диаграммам. Это происходит в силу Того, что временная задержка сц между началами этапов г и / является, вообще говоря, постоянной для данного i и совершенно не зависит от следующего этапа. Редкие исключения всегда можно учесть, вводя некоторые фиктивные этапы. В таких случаях подобное представление приводит на практике к более простым графам (даже с учетом фиктивных вершин), в то время как представление, рассмотренное ранее, остается неизменным. Другой особенностью практического использования метода ПЕРТ является то, что интервалы времени (т. е. временные задержки) между этапами считаются случайными величинами, а не детерминированными, как считалось здесь.

Задачи планирования, решаемые с помощью метода ПЕРТ, не учитывают наличие ресурсов и не рассматривают потребности этапов в ресурсах. Вместо этого производится (после нахождения критического пути такое распределение ресурсов по этапам проекта, при котором задерживается выполнение этапов, не принадлежащих критическому пути. Если же ограничения на ресурсы учитывать на стадии планирования, то задача из очень легкой превращается в очень трудную [1, 30, 37] и решить ее удается лишь для размерностей на 3-4 порядка меньших, чем в случае соответствующей задачи без ограничений.

7. Задачи, близкие к задаче о кратчайшем пути

В алгоритме Флойда нахождения кратчайшего пути между всеми парами вершин (см. разд. 3 настоящей главы) была использована трехместная операция (8.5). Применение этой операции п раз к матрице весов [сц] дает заключительную матрицу, элементы которой равны длинам кратчайших путей. Эта операция является частным случаем более общей трехместной операции

Zij = OPT:iZij,Ziu®Zkj], (8.8>

где Z - функция пути, подлежащая оптимизации, а ® - некоторая общая операция. Операция ® налагает единственное ограничение в случае ее применения к различным задачам нахождения кратчайших путей в графах. А именно если путь от Xi к Xj проходит через промежуточную вершину х^ и z - некоторая характеристика пути, на которой базируется оптимизация, то для ® должно выполняться условие

Z£j = z<ft®Zfej. (8.9)

Ниже приводится несколько примеров использования этой операции.

7.1. Наиболее надежный путь

В задаче о кратчайшем пути в качестве длины пути бралась сумма весов дуг, образующих этот путь. Рассмотрим теперь случай, когда вес дуги представляет ее надежность. Надежность пути от S к t, составленного из дуг, взятых из множества Р, дается формулой

Р() = Ц.)ерР' -

где - надежность дуги (х;, Xj), т. е. вероятность ее существования в графе (или - в случае физических систем - вероятность того, что она находится в работоспособном состоянии).

Задачу нахождения наиболее надежного пути от s к можно свести к задаче о кратчайшем пути от s к t, взяв в качестве веса -Cij дуги {xi, Xj) величину С;у = - log pij. Прологарифмировав обе-части соотношения (8.10), получим

l0gp(P)= S l0gpiy= - 2 Cij.

(X., Х^)6Р (Xj, Xj.)6P

Отсюда видно, что кратчайший путь от s к t с матрицей весов [с;у] будет в то же время и наиболее надежным путем с матрицей: Ipij], а надежность этого пути равна антилогарифму его длины..