При другой формулировке задачи о наиболее надежном пути возможно непосредственное использование трехместной операции; а именно операция вводится с помощью соотношения

Pг^ = шax[pг^ , pik-pkj].

В качестве начальной [рг/]-матрицы берется матрица надежностей дуг, причем нулевые элементы указывают на отсутствие соответствующих дуг. Такая формулировка позволяет, очевидно, найти наиболее надежные пути между всеми парами вершин.

7.2. Путь с наибольшей пропускной способностью

В этой задаче каждая дуга (х,-, Xj) графа имеет пропускную способность и требуется найти путь от s к с наибольшей пропускной способностью. Пропускная способность пути Р определяется, конечно, дугой из Р с наименьшей пропускной способностью, т. е.

Q{P) min [gtj]. (8.11)

Теорема 1 ). Пропускная способность пути с наибольшей пропускной способностью от s к t равна

min{ max [Яц]}, к (X., х.)ек

где К - любой (s-tVpaapea (в множестве дуг).

Доказательство. Пусть Q - пропускная способность пути с наибольшей пропускной способностью. Так как каждый путь от S к должен содержать по крайней мере одну дугу из каждого (5-)-разреза, то для каждого разреза К будет выполняться неравенство

max [qi}]Q. (8.12)

(Я., х.)К'

Поскольку в каждом ( -)-пути должна присутствовать по крайней мере одна дуга с пропускной способностью, не превосходящей Q, и поскольку, взяв по одной такой дуге из каждого (s-i)-nyTH, мы получаем некоторый ( -)-разрез (по определению), то существует хотя бы один разрез, скажем К', для которого

max [?г, ]<(?. (8.13)

(ЗС., xj)eK

Таким образом, разрез К, доставляющий минимум выражению

min{ max [дц]}, (8.14) к (X., xj)eK

1) Обратите внимание иа сходство теоремы 1 с теоремой о максимальном потоке и минимальном разрезе из гл. 2; на самом деле теорема 1 является минимаксным вариантом последней.

должен одновременно удовлетворять неравенствам (8.12) и (8.13), т. е. для него должно выполняться равенство. Отсюда следует справедливость теоремы.

Очевидный алгоритм нахождения пути с наибольшей пропускной способностью, основанный на теореме 1, состоит в следуюш,ем.

Шаг 1. Начать с ( --разреза К = ({ }, X- { }) и найти наибольшую пропускную способность Q дуг из К.

Шаг 2. Построить остовный подграф G = (X, А'), где А' =

Шаг 3. Найти множество R (s) вершин, достижимых из s в графе А'. (Построение множества R (s) описано в гл. 2.)

Шаг 4. Если t R (s), то = (? и любой (s -<)-путь в остовном подграфе G будет иметь наибольшую пропускную способность, равную Q. Если t R (s), перейти к шагу 5.

Шаг 5. Взять в качестве К разрез (R (s), X - R (s)) и найти наибольшую пропускную способность Q дуг в этом новом разрезе. (Текущее значение величины Q меньше, чем предыдущее, в силу определения множества R (s) на шаге 3 и множества дуг А' на шаге 2.) Возвратиться к шагу 2.

Для неориентированных графов G Франк и Фриш [16] предложили еще более простую процедуру нахождения пути с наибольшей пропускной способностью, состоящую в следующем.

Пусть Ki - некоторый (5-<)-разрез, & Q - наибольшая пропускная способность ребер из Ку. Если теперь закоротить любое ребро {Х{, Xj) с пропускной способностью qij Q, т. е. вершины xi и Xj заменить одной вершиной х, положив

Г (х) = Г (х,) и Г (Xj), (х) = Г-1 (Xi) и Г-1 (Xj),

и ребро (xi, Xj) удалить, то получившийся граф будет иметь тот же самый путь с наибольшей пропускной способностью, что и первоначальный граф G. Справедливость этого утверждения вытекает из того факта, что Q является верхней границей для Q (в соответствии с (8.12)), и, следовательно, ребра cqijQ не могут повлиять на оптимальное решение, т. е. не могут войти в разрез К. Поскольку закорачивание ребра (х;, Xj) может повлиять только на разрезы, содержащие {xt, Xj) (зти разрезы удаляются), то разрез К графа G (или все разрезы, доставляющие минимум выражению (8.14), если их несколько) будет также и разрезом преобразованного графа Gi.

Процедуру, примененную к первоначальному графу G, можно повторить и для графа Gi, выбирая другой (5-<)-разрез ij, зако-

рачивая все ребра из Gi, пропускная способность которых не меньше наибольшей пропускной способности любого ребра из К2- Это дает граф и т. д. Процесс закончится, когда будут закорочены s и t. Теперь каждый (5-<)-путь в графе G, образованный вершинами из G и теми ребрами, которые оказались закороченными, будет иметь максимально возможную пропускную способность Q. Ограничение на применимость данного алгоритма только к неориентированным графам вызвано именно процессом закорачивания , так как при этом неявно предполагается, что путь с пропускной способностью, не меньшей, чем существует между любыми вершинами (двумя или большим числом), заменяемыми в описанном процессе единственной вершиной, но такое предположение может не выполняться, если закорачиваемые ребра имеют ориентацию.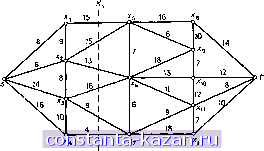

Рис. 8.6а. Граф из примера 7.2.1.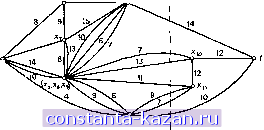

Рис. 8.66. Граф после первого стягивания.