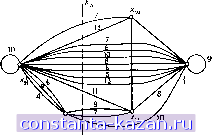Рис. 8.6в. Граф после второго стягивания. X, 15 Xj 16 -fg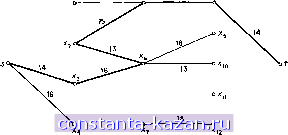

Рис. 8.6г. Граф G и путь с наибольшей пропускной способностью.

7.2.1. Пример. Задача состоит в нахождении (s-f)-nytn (s) наибольшей пропускной способности в неориентированном графе, изображенном нгг рис. 8.6а, где пропускные способности ребер указаны числами, стоящими у этих ребер.

Выбрав произвольно (5-)-разрез К^, показанный на рис. 8.6а пунктиром, найдем, что ребром с максимальной пропускной способностью в К будет (xg, Xq) с g-g.e = 16. Закорачивая все ребра с пропускной способностью 16, получим граф Gi, изображенный на рис. 8.66. Выберем теперь (5-)-разрез К2 графа так, как показано пунктиром на рис. 8.66. Наибольшая пропускная способность ребер в равна 14. Поэтому закорачиваем все ребра с пропускной способностью 14 и получаем граф Gj, изображенный на рис. 8.6в. Беря в качестве следующего (5-)-разреза Kg - он показан пунктиром на рис. 8.6в,- получаем = 13, а в по-

строенном графе (полученном из носле закорачивания всех ребер с пропускной способностью 13) вершины s и t будут закорочены.

Окончательным графом G будет остовный подграф графа G, содержащий лишь те ребра, которые закорачивались во время; описанной процедуры (т. е. только ребра {Xi, Xj) с ди13). Этот последний граф изображен на рис. 8.6г и видно, что существует-только один (s-f)-nyTb с наибольшей пропускной способностью. Этот путь показан жирными линиями, причем критическим ребром, этого пути будет (х^, х^) с пропускной способностью 13.

Если требуется найти пути с наибольшей пропускной способностью между каждой парой вершин графа, то трехместную операцию из выражения (8.8) можно использовать в форме

qij = max[gi}, ram{gtj gj}], (8.15>

поскольку так введенная операция удовлетворяет требованиям налагаемым соотношением (8.9). Начальной матрицей gij] является исходная матрица пропускных способностей дуг (с нулевыми элементами на местах отсутствующих дуг); конечная матрица Igij] дает пропускные способности путей между всеми парами: вершин.

7.3. Путь с наибольшей приведенной пропускной способностьн>

Рассмотрим граф G, в котором каждой дуге (Xj, Xj) приписаньк два числа ри и qtj, представляющие соответственно надежность и пропускную способность дуги. Задача нахождения пути от s-к t с наибольшей приведенной пропускной способностью является комбинацией двух последних задач о путях, обсуждавшихся выше-в разд. 7.1 и 7.2. Если приведенную пропускную способность пути Р обозначить через е (Р), то задача состоит в нахождении пути, минимизирующего выражение

е{Р)= П Pij-i min М. (8.16)

в этом слзгчае нельзя воспользоваться трехместной операцией^ так как не удается найти оператора ®, который (для пути от х„ к Хь через верпшну х^) удовлетворяет условию Саь = ос ® сь-

Несуществование такого оператора можно обосновать следующим образом:

еаь^ П Ри- [4t}] =

= П Pu- и Ргг™п{ min [qtj], min [gj]},

iXf, xj)£a-c (Xf 3c,)ec-*b (X., Xj)£ae (ж., ж^)ес-Ь

Следовательно,

Cab = min [РисСсЫ РсЬ^ас]- (8.17>

Из этого выражения видно, что так как надежности и р^ь не могут быть выражены на языке величин вас, е^ь, Ptj и Qij, то невозможно найти оператор, удовлетворяюпций обпцим условиям

z:?=10,p = 0,6 2:9=20, р=0,7

у=8, р=0.7 (1=9, р = 0,8

Рис. 8.7.

(8.9) и, следовательно, невозможно непосредственно использовать, трехместную операцию.

На самом деле нетрудно показать, что оптимальный путь от Хд к Хь через х^ не зависит от:

(i) оптимальных путей от Ха к и от х^ к х;,;

(11) путей наибольшей пропускной способности от Ха к х^ и от Хс к х^;

(iii) путей наибольшей надежности от Ха к х,. и от Xg к Xj или любой их комбинации.

В этом можно убедиться, рассматривая рис. 8.7, на котором изображены пути всех трех вышеуказанных типов от Ха к Xg Pi от Хс к Хь, причем оптимальное значение величины е, которое можно получить с помопцью некоторой комбинации этих путей, равно 4,20. На рисунке изображены, кроме того, такие два пути от Ха к Хс и от Хд К Xj, НИ ОДИН ИЗ которых НО является оптимальным в любом из трех вышеприведенных смыслах, между их соот-ветствуюпцими конечными вершинами. Однако эти два пути образуют оптимальный путь между вершинами Хд и Xj, которому отвечает значение величины е, равное 4,48.

где запись а 6 и т. д. применяется как для пути от Ха к Хь> так и для множества дуг этого пути. Вводя обозначения

Рас= П Ро-, РсЬ= П РО

Qac min [qij], icb= min [q], можем записать