 |
 |
 |
 |
|
Главная -> Гамильтоновы циклы 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 [ 69 ] 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 8. Задачи 1. Найти кратчайшие пути от вершины 1 ко всем другим вершинам графа на рис. 8.10. Изобразить также 1-базу. 2. Используя метод из разд. 2.2, найти кратчайшие пути от вершины 1 ко всем другим вершинам графа, изображенного на рис. 8.11. 3. Решить задачу 2, изменив вес ребра (4,5) с 8 на -8. Выявить все отрицательные циклы. 4. Граф на рис. 8.12 представляет сеть допустимых маршрутов для некоторого судна. Каждая дуга имеет пометку (а, Ь), причем а равно выгоде, получаемой при обслуживании этого маршрута, а 6 - времени обслуживания маршрута. Найти наиболее выгодный (в терминах скорости оборота капитала) маршрут судна. 5. Для графа, изображенного на рис. 8.10, найти четыре кратчайшие простые цени от вершины 1 к вершине 10. Найти кратчайшую простую цепь из 5 дуг от вершины 1 к вершине 10. 6. На рис. 8.13 изображена диаграмма ПЕРТ. Продолжительность операции i дается числом, стоящим у дуги, исходящей из соответствующей вершины i. Найти критический путь и такую максимально возможную задержку начала выполнения операции 5, которая не приведет к задержке реализации всего проекта. Путь Р- С наибольшей надежностью в графе G показан на на рис. 8.8 жирными линиями. Здесь р = 0,504, (?- = 10 и, следовательно, приведенная пропускная способность этого пути равна е = 5,04. Удаляя из G все дуги с пропускными способностями 10, получим графС, изображенный на рис. 8.9а. Путь Р'р с наибольшей надежностью в графе G показан на рисунке жирными линиями. Для этого пути р = 0,454, Q = 14 и, значит, приведенная пропускная способность пути Р' равна е = 14 х X 0,454 = 6,36, что больше полученной ранее величины (5,04) и, следовательно, заменяет ее. Удаляя из G все дуги с пропускной способностью 14, получаем граф G , изображенный на рис. 8.96. В этом графе суш;ествует только один путь между s и Z; р = 0,141, Q - = 15 и, следовательно, приведенная пропускная способность равна 2,12, что хуже, чем лучшее предыдуш;ее значение этой величины. Удаляя все дуги с пропускной способностью 15 из G , мы разъединим вершины s и t, так что лучший нредыдуш;ий ответ, т. е. путь (s, 1, 2, 5, t), с приведенной пропускной способностью 6,36 будет оптимальным ответом. 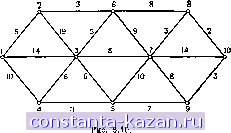 2 -14 3 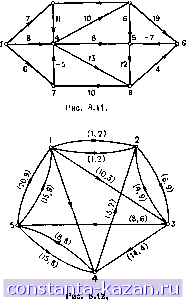 7. В графе, изображенном на рис. 8.14, каждое ребро имее пометку (а, Ъ), где а - пропускная способность, а 6 - надежность ребра. Найти: (а) путь с наибольшей пропускной способностью от вершины i к вершине 10; (б) путь с наибольшей надежностью от вершины 1 к вершине 10{ (в) путь с наибольшей приведенной пропускной способностью от вершины 1 к вершине 10 Конец 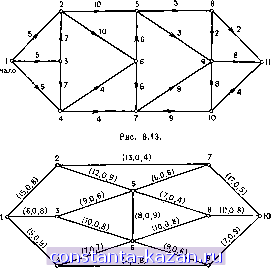 Рис. 8.14. 8. Для того случая, когда веса всех дуг неотрицательны, модифицировать алгоритм Дейкстры так, чтобы расстановка пометок происходила одновременно и от вершины s, и от вершины t Уделить особое внимание правилу окончания процедуры (см. 129), [28]). 9. Доказать, что ответ, полученный по алгоритму Флойда, описанному в разд. 3.1, является оптимальным, и показать, что объем вычислений растет как О (га*) (см. [7(). |
|
© 2025 Constanta-Kazan.ru
Тел: 8(843)265-47-53, 8(843)265-47-52, Факс: 8(843)211-02-95 |