Из определений сразу же следует, что односторонние компоненты графа могут иметь общие вершины. Сильная компонент должна содержаться по крайней мере в одной односторонней компоненте, а односторонняя компонента содержится в некоторой слабой компоненте данного графа G.

8. Матричные представления

Для алгебраического задания графов удобно использовать следующие матрицы.

8.1. Матрица смежности

Пусть дан граф G, его матрица смежности обозначается череа А = [aij] и определяется следующим образом:

aij = i, если в G существует дуга (Xi,xj),

aij = Q, если в G нет дуги {Xi,Xj).

Таким образом, матрица смежности графа, изображенного на рис. 1.8, имеет вид

Матрица смежности полностью определяет структуру графа. Например, сумма всех элементов строки Xi матрицы дает полустепень исхода вершины Xj, а сумма элементов столбца - полустепень захода вершины Zj. Множество столбцов, имеющих 1 в строке Xi, есть множество Г (zj), а множество строк, которые имеют 1 в столбце Xi, совпадает с множеством Г (Zj).

Возведем матрицу смежности в квадрат. Пусть элемент а\-матрицы А* определяется по формуле

(1.14)

Слагаемое в уравнении (1.14) равно 1 тогда и только тогда, когда оба числа а^ и а^ равны 1, в противном случае оно равно 0.

Поскольку ИЗ равенств а<у = а^ = 1 следует существование пути длины 2 из вершины Xt к вершине Xft, проходящего через вершину Xj, то ajft равно числу путей длины 2, идущих из Xi в аг.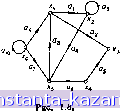

Аналогично если а|Р' является элементом матрицы А**, то а^Р) равно числу путей (не обязательно орцепей или простых орце-пей) длины р, идущих от Xj к Xft.

8.2. Матрица инциденций

Пусть дан граф Gere вершинами и т дугами. Матрица инциденций графа G обозначается через В = [bij] и является матрицей размерности п X т, определяемой следующим образом: bj/ = 1, если Х{ является начальной вершиной дуги uj, bfj = -1, если Xi является конечной вершиной дуги ау, bi] ~ О, если Xi не является концевой вершиной дуги или если aj является петлей.

Для графа, приведенного на рис. 1.8, матрица инциденций имеет вид

Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каж-

дый столбец либо содержит один элемент, равный 1, и один - равный -1, либо все элементы столбца равны 0.

Если G является неориентированным графом, то его матрица инциденций определяется так же, как и выше, за исключением того, что все элементы, равные -1, заменяются на +1.

9, Задачи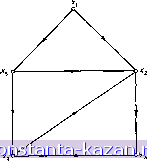

Рис. 1.9.

1. Для графа, приведенного на рис. 1.9, найти

(а) Г (хг), (д) do (х^),

(б) Г-1 (х,), (е) dt (хз),

(в) Р (xg), (ж) матрицу смежности А,

(г) Г-2 (xj), (з) матрицу инциденций В.

2. Для графа G - {X, А), изображенного на рис. 1.9, описать

(а) порожденный подграф ({х^, Xj, Х4, х^}),

(б) остовный подграф {X, А'), где (х^, ху) А' тогда и только тогда, когда i + / нечетно,

(в) остовный подграф подграфа из (а), определенный так же, как в пункте (б).

3. Для неориентированного графа доказать, что в нем число вершин с нечетной степенью четно. (Нуль - четное число.)

4. Показать, что любой полный симметрический граф содержит гамильтонов цикл.