Глава 9

ЦИКЛЫ, РАЗРЕЗЫ И ЗАДАЧА ЭЙЛЕРА

1. Введение

Целью настоящей главы является изучение циклов в графа и исследование некоторых из их свойств и связей с другими понятиями (такими, как понятие дерева), введенными ранее. Два тип циклов в графах эйлеровы и гамильтоновы циклы, часто встречаются в практических задачах и поэтому представляют особый интерес. Первые из них рассмотрены в настоящей главе, а вторые - в следующей.

В настоящей главе мы будем заниматься циклами как в ориентированных, так и в неориентированных графах, а также в муль-тиграфах, являющихся слабым обобщением понятия графа. Последние являются графами, в которых может существовать несколько дуг (xf, х/) между двумя данными вершинами Ж| и Х). Если наибольшее число запараллеленных дуг равно s, то граф навывается s-графом. Так. на рисунке 9.1 представлен 3-граф. Очевидно, что обычный граф можно рассматривать как 1-граф.

s-Графы очень часто возникают на практике, когда граф используется для представления физической системы в естественных науках, вопросах управления, инженерном деле и т. д. Так, например, 3-граф на рис. 9.1 изображает молекулярную структуру органического химического соединения акрилонитрила. В электротехнике графы, изображающие электрические цепи, почт всегда являются s-графами, так как параллельно может быть включено несколько электрических компонентов. В проблемах надежности оборудования или сетей связи наиболее важные устройства или линии связи часто дублируются, утраиваются ИТ. д., а возникающая избыточность увеличивает надежность системы. Графы таких систем также являются s-графами.

2. Цикломатвческое число и фундаментальные циклы

Пусть G - неориентированный s-граф с п вершинами, т ребрами и р связными компонентами. Определим число р (G) как

p(G) = n-p, (9.1>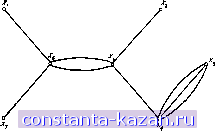

Рис. 9.1.

р (<т) и V {G) имеют прямой физический смысл. Так, цикломатиче-ческое число равно наибольшему числу независимых контуров в графе электрической цепи, т. е. наибольшему числу независимых круговых токов, которые могут протекать в цепи. Коцикло-матическое число равно наибольшему числу независимых разностей потенциалов между узлами электрической цепи.

Рассмотрим, например, электрическую цепь, показанную на рис. 9.2а. Неориентированный граф G этой цепи состоит из един-ственной связной компоненты (р = 1) и изображен на рис. 9.26, где остов Т показан жирной линией (см. гл. 6).

Добавление любого ребра (xj, xj) из G, не принадлежащего Г, к ребрам дерева Т приводит к образованию точно одного (простого) цикла, состоящего из ребер остова Т, лежащих на (единственной) цепи из xj в Xi, и только что добавленного ребра. Например, добавляя ребро а, = {xi, х^), получаем цикл {xi, х Xg, х^, х^, х^. Так как в графе G имеется т ребер, п - 1 из которых лежат в Т, то число всех циклов, построенных таким способом, равно т - п -\--Ь 1, что совпадает с цикломатическим числом графа G. В примере на рис. 9.2 число таких циклов равно 15 - 7 1 = 9, они изображены на рисунке пунктирными линиями и обозначены через

р (С) дает тогда полное число ребер в остовах каждой из р связных компонент графа G.

Число v (G) определяется как

v(G) = m - p(G) = m - n + p (9.2)

и называется цикломатическим числом (иногда его называют также дефектом или первым числом Ветти), а число р (G) называется коцикломатическим числом.

В теории электрических цепей (и на самом деле при представлении любой системы с сосредоточенными параметрами) числа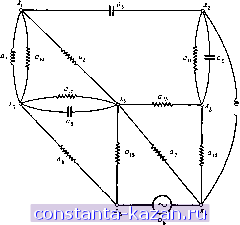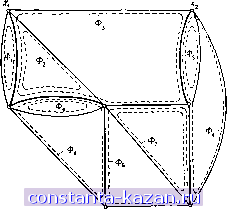

Рис. 9.2. (о) Электрическая цепь, (б) Фундаментальные циклы.