Фх, Фг, . . ., Ф9. Все эти циклы, очевидно, независимы между еобой, чак как каждый из них имеет но крайней мере одно ребро, не принадлежащее никакому другому циклу. В общем случае V (G) циклов, получаемых добавлением какого-либо ребра из G, не лежащего в Г, к ребрам Т, называются фундаментальными циклами. Если семейство этих циклов обозначить через Ф (в нашем примере Ф = {Фх, Фг, . . ., Ф }), 10 любой другой цикл н графе, не принадлежащий к Ф, может быть выражен в виде линейной комбинации циклов из Ф, если принять следующее оглашение [21].

Пусть каждый фундамеетальный цикл Ф{, г = 1, . . ., v представлен т-мерным вектором, в котором /-я комнонента равна 1 или О в зависимости от того, принадлежит ли /-е ребро данному циклу. Тогда, используя Ф как символ сложения по модулю 2, любой цикл Фй можно представить как сзшму по модулю 2 фундаментальных циклов. Так, цикл Фю = ( з, ц, 14, в, 8 i) на рис. 9.2(6) может быть представлен в виде

Фю = Ф1 Ф Фз Ф Фб Ф Фв

= (100000000100000) ф (001000000111100)

Ф (000001000000111) ф (000000010001001) = (101001010010010)

Отметим, что обращение вышеприведенного утверждения неверно, а именно некоторая сзшма но модулю 2 фундаментальных циклов не обязательно дает единственный цикл, но может представлять два и более циклов. Например, сумма Ф^® Ф3 Ф Фв Ф Ф7 соответствует двзш циклам {а^, з, ц, а^з) и {а^, ат, ais). Таким образом, для порождения всех циклов графа G не надо брать все 2У<в) - I комбинаций фундаментальных циклов и складывать их но модулю 2: некоторые из этих сумм на самом деле не будут циклами Более того, если данная сзма, скажем Ф^ ф Ф; ф Ф^ ф .. не порождает цикла, то нельзя отбросить другие сувош, ее содержащие, так как, складывая по модулю 2 cjrMMy Ф; ф Ф^ ф Ф^ ф. . . с другой сзшмой, например Фа Ф ФрФ ФуФ ... (которая самл может не порождать цикла), мы можем получить цикл. Для преодоления этой трудности Уэлч [26] предложил некоторый метод, позволяющий отбрасывать некорректные комбинации фундаментальных циклов, как только они появляются. Этот метод основан на упорядочении фундаментальных циклов в соответствии со специальным множеством правил.

Следует также заметить, что, хотя число фундаментальных циклов равно v (G), сами эти циклы определены неоднозначно я аависят от первоначально выбранного остова Т. Действительно,

в графе G можно найти множество из v (G) независимымх циклов, которые нельзя получить добавлением ребер к дереву, как это делалось выше. О таком множестве не следует говорить, что оно

Рис. 9.3. Независимые, но нефундаментальные циклы.

фундаментальное . На рис, 9.3 показано множество из v (G) = 9 независимых циклов графа G, которое не может быть получено добавлением ребер ни к какому остову графа G и которое поэтому не будет фундаментальным множеством.

3. Разрезы

Понятие разреза очень тесно связано с понятием цикла и опрв-деляется так.

Определение. Бели вершины неориентированного графа G = - {X, А) разбиты на два множества Хо и Хо (где Хо с: X и Х- является дополнением Хо относительно X), то множество ребер ррафа G, одни концевые вершины которых лежат в Хо, а другие - в Хо, называется разрезом графа G.

Множество ребер разреза может быть представлено множеством верпшн пары (Хо, Хо). Таким образом, остовный подграф G == (X, А - (Хо, Хо)), полученный из G удалением ребер, принадлежащих разрезу, является несвязным графом, состоящим ао крайней мере из двух компонент, В графе на рис. 9.4 множе-

СТВО ребер, показанных пунктиром, образует разрез, определяемый множествами Zo = {х; [ г = 1, . . ., 4} и Хд = {xf \ i = = 5, . . ., 11}. Получающийся остовный подграф состоит из четырех связных компонент:

(Xl, Xz, Хз, Xi), (Xs, Xf X-i), {Xa) и {Xg, Xio, Xii).

Множество ребер S, удаление которых из графа G дает несвязный остовный подграф Gp = {X, А - S) я при этом не существует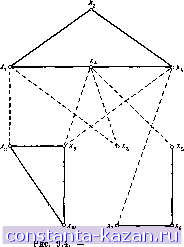

--разрез (Хо, Хо).

никакого собственного подмножества S cz S, такого, что граф Gp = {X, А - S) также несвязен, называется правильным разрезом. Это множество можно также представить парой (Zo, Zo), хотя теперь остовный подграф, полученный удалением правильного разреза из G, разбивает G точно на две связные компоненты, одна из которых имеет своими верпганами множество Zo, а другая - множество Zq. В общем случае каждый разрез является объединением некоторого числа правильных разрезов. В графе на рис. 9.4, например, разрез, показанный пунктиром, является объединением трех правильных резрезов: {{xi, Хц), (х^, х^), (xg, 3:9)},