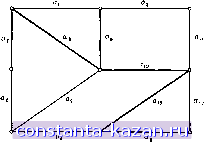Рис. 9.7.

матрица фундаментальных разрезов равна

где разрезы Z;, соответствующие ребрам остова, имеют номера v (G) + i = 5 + г, i = 1, 2, . . ., 8.

Существует несколько интересных соотношений между матрицами циклов, разрезов и инциденций. Ниже все арифметические операции являются операциями по модулю 2. Здесь мы будем рассматривать неориентированные графы без петель.

Теорема 2. Матрица инциденций В и транспонированная матрица фундаментальных циклов Ф* ортогональны, т. е. В-Ф' = 0.

Теорема 3. Матрица фундаментальных циклов Ф и транспонированная матрица фундаментальных разрезов К' ортогональны, т. е. Ф.К' = 0.

5. Эйлеровы циклы и задача китайского почтальона

Определение. Если дан неориентированный s-граф G, то эйлеров цикл (эйлерова цепь) - это такой цикл (цепь), который проходит ровно один раз по каждому ребру.

Очевидно, не все графы имеют эйлеровы циклы (см., например, граф на рис. 9.8), но если эйлеров цикл существует, то это озна-

Рис. 9.8. Граф без эйлерова цикла.

Эти две теоремы являются немедленным следствием двух очевидных фактов:

(1) Каждая вершина в цикле инцидентна четному числу ребер (а в случае простого цикла - двум ребрам) этого цикла.

(2) Каждый разрез цикла, индуцированный некоторым разрезом, имеет четное число ребер, обЩИх с этим разрезом.

Теорема 2 следует из (1), а теорема 3 - из (2), если вспомнить, что все операции рассматриваются по модулю 2, так что, например, 2 = 0 (mod 2). Кроме того, существуют доказательства этих теорем [21, 17, 6], не использующие предположения о фундаментальности циклов и разрезов. Следовательно, сформулированные теоремы справедливы для любых матриц циклов и разрезов. Последние определяются аналогичным образом.

По теореме 3 можно написать

ФК = (I I Ф,2) .(Щ^)=К1 + Ф,2 = 0.

Поэтому

К1.= -Ф,2 = Ф,2, (9.3)

так как -1 = 1 (mod 2). Вследствие этого матрица фундаментальных разрезов может быть немедленно получена, как только известна матрица фундаментальных циклов, и наоборот. Справедливость соотношения (9.3) можно проверить на приведенных выше матрицах Ф и К для графа, изображенного на рис. 9.7.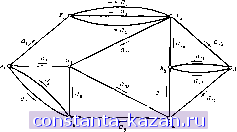

Рис. 9.9.

чает, что, следуя вдоль этого цикла, можно нарисовать граф на бумаге, не отрывая от нее карандаша. 3-граф на рис. 9.9 имеет следующий эйлеров цикл (начиная с вершины Xi):

aiaiaaaaisO-uaiaaiaiiaiQanaigagasasaTae.

Направление движения по каждому ребру показано на рисунке стрелками.

Эйлер первым в своей знаменитой задаче о Кёнигсбергских мостах рассмотрел вопрос о существовании таких циклов в графах.

(а) (б)

Рис. 9.10. (о) Карта Кенигсберга, (б) Эквивалентный граф.

Кенигсберг (теперь Калининград) расположен на обоих берегах реки Преголя и на двух островах этой реки. Берега реки и два острова соединены семью мостами как показано на карте на рис. 9.10 (а).

Вопрос - поставленный в 1736 году - состоит в том, можно ли, начав с некоторой точки, совершить прогулку и вернуться