между любыми двумя вершинами, т. е. оптимальный цикл не проходит ни по какому ребру графа G более чем два раза.

5.2.2. Пример. Рассмотрим граф G, изображенный на рис. 9.12, имеющий 12 вершин и 22 ребра, веса которых указаны у каждого ребра. Задача состоит в нахождении цикла, проходящего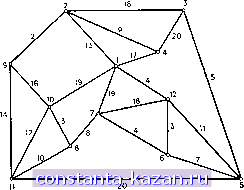

Рис. 9.12. Граф из примера 5.2.2.

по каждому ребру G по крайней мере один раз и имеющего минимальный вес. Множество вершин нечетной степени этого графа есть {1, 3, 4, 6, 8, 9}. Используя алгоритм кратчайшей цепи Дейкстры (см. гл. 8), найдем матрицу D из шага 1:

На шаге 2 алгоритм минимального паросочетании (см. гл. 12) связывает следуюш,ие вершины (два других паросочетании также являются минимальными):

1 с 6, цепь 1-12-6, вес 7,

3 с 8, цепь 3-5-6-7-8, вес 24,

9 с 4, цепь 9-2-4, вес И.

Граф G~ (М*), получающийся после выполнения шага 3, изображен на рис. 9.13; пунктиром показаны искусственные ребра.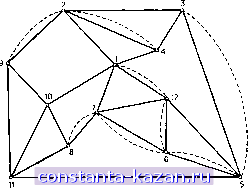

Рис. 9.13. Граф G- (М*) из примера 5.2.2. - реальные ребра;--- искусственные ребра.

Из этого рисунка видно, что оптимальный цикл в графе G проходит череэ ребра (9, 2), (2, 4), (3, 5), (5, 6), (1, 12), (12, 6), (7, 6) и (8, 7) дважды, а через все остальные ребра - один раз. Вес этого цикла равен 294.

Как только найден граф G~ {М*}, могут быть сразу же найдены по алгоритму Флёри, упомянутому ранее, эйлеров цикл этого графа и соответствующий оптимальный цикл, проходящий по первоначальному графу G. Для графа, изображенного на рис. 9.13, например, один из возможных эйлеровых циклов, полученных по вышеприведенному правилу, дается последовательностью вершин (начиная с вершины 1):

1, 4, 3, 5, 3, 2, 4, 2, 1, 12, 5, 6, 7, 8, 10, 1, 7, 6, 12, 6, 5, И, 9, 2, 9, 10, И, 8, 7, 12, 1.

) Реберный граф графа G часто обозначается через L (G).- Прим. ред.

Этот цикл является также соответствующим оптимальным диклом, проходящим по первоначальному графу из рис. 9.12. Возможны также другие оптимальные циклы, проходящие ребра графа в ином порядке. Однако эти циклы будут проходить дважды по тому же множеству из 8 ребер. Таким образом, как только определены те ребра графа G, по которым оптимальный цикл проходит дважды, можно построить несколько таких циклов в графе G.

5.3. Связь между эйлеровыми и гамильтоновыми циклами

Гамильтонов цикл в графе G был определен в главе 1 как простой цикл, проходящий (один, и только один раз) через каждую вершину графа G. Не удивительно, что двойственность между эйлеровыми и гамильтоновыми циклами (замена вершины на ребро и наоборот) приводит к тесной связи между этими двумя понятиями в применении к неориентированному графу G и соответствующему ему реберному графу, определяемому ниже.

Определение. Реберный ) граф графа G имеет столько же вершин, сколько ребер у графа G. Ребро между двумя вершинами графа Gi существует тогда и только тогда, когда ребра графа G, соответствующие этим двум вершинам, смежны (т. е. инцидентны одной и той же вершине графа G).

Например, для графа, показанного на рис. 9.14(a), граф G, изображен на рис. 9.14(6).

Легко можно показать [15], что верны два следующие утверждения о взаимоотношении между эйлеровыми и гамильтоновыми циклами.

(1) Если G имеет эйлеров цикл, то Gj имеет как эйлеров, так и гамильтонов циклы.

(2) Если G имеет гамильтонов цикл, то Gj также имеет гамильтонов цикл.

Обращение этих утверждений, как нетрудно продемонстрировать, неверно. Для графа, изображенного на рис. 9.14(a), степени всех его вершин четны и поэтому существует эйлеров цикл. Таким образом, граф Gj, изображенный на рис. 9.14(6), также имеет эйлеров цикл (поскольку степени всех его вершин опять четны) и, кроме того, имеет гамильтонов цикл, задаваемый последовательностью вершин а, g, с, d, е, /, Ъ, h, i, а. Если теперь из графа G удалить ребро Ь, то новый граф G не имеет эйлерова цикла, но все еще имеет гамильтонов цикл 1, 2, 6, 5, 4, 3, 1. Реберный граф Gi графа G является тогда графом из рис. 9.14 (б) с удаленной вершиной b (и без ребер, инцидентных вершине Ь). Этот граф все еще имеет гамильтонов цикл а, /, е, d, с, g, h, i, а.