ответом на задачу i). Если же решение имеет бесконечное значение, ТО G не имеет гамильтонова цикла. С другой стороны можно дать еще одну интерпретацию задачи i). Рассмотрим снова полный орграф Gi с общей матрицей весов дуг [с^] и рассмотрим задачу нахождения такого гамильтонова цикла, в котором самая длинная дуга ) минимальна. Эту задачу можно назвать минимаксной задачей коммивояжера, оттеняя ее минимаксную природу (по сравнению с классической задачей коммивояжера), которую в той же терминологии можно было бы назвать минисуммной задачей. Покажем теперь, что задача (i) действительно эквивалентна минимаксной задаче коммивояжера.

В вышеупомянутом полном орграфе Gi мы можем наверняка найти гамильтонов цикл. Пусть это будет цикл Ф^, и пусть вес самой длинной его дуги равен с^. Удалив из Gi любую дугу, вес которой не меньше с^, получим орграф G. Найдем в орграфе Gj гамильтонов цикл Ф^, и пусть вес его самой длинной дуги равен Cj. Удалим из G2 любую дугу, вес которой не меньше Cj, и так будем продолжать до тех пор, пока не получим орграф G+i, не содержащий никакого гамильтонова цикла. Гамильтонов цикл Фт в Gm (с весом с^) являстся тогда по определению решением минимаксной задачи коммивояжера, так как из отсутствия гамильтонова цикла в Gm+i следует, что в Gi не существует никакого гамильтонова цикла, не использующего по крайней мере одну дугу с весом, большим или равным с^. Таким образом, алгоритм нахождения гамильтонова цикла в орграфе решает также минимаксную задачу коммивояжера. Наоборот, если мы располагаем алгоритмом решения последней задачи, то гамильтонов цикл в произвольном орграфе G может быть найден с помощью построения полного орграфа Gi с тем же самым множеством вершин, что и в G, дугам которого, соответствующим дугам из G, приписаны единичные веса, а остальным дугам - бесконечные веса. Если решение минимаксной задачи коммивояжера для Gi имеет конечный вес (на самом деле равный единице), то в графе G может быть найден соответствующий гамильтонов цикл. Если же решение имеет бесконечный вес, то в графе G не существует никакого гамильтонова цикла. Следовательно, две указанные задачи можно рассматривать как эквивалентные, поскольку было продемонстрировано, что алгоритм нахождения гамильтонова цикла позволяет решать минимаксную задачу коммивояжера и наоборот.

Ввиду того что обе сформулированные выше задачи (i) и (ii) часто встречаются в практических ситуациях и (как мы увидим позже) задачу (i) саму по себе решить намного проще, чем как подзадачу задачи (ii), мы обе эти задачи рассмотрим отдельно в частях I и II настоящей главы.

) То есть дуга с наибольшим весом.- Прим. ред.

часть I

2. Гамильтоновы циклы в графе

Пока неизвестно никакого простого критерия или алгебраического метода, позволяющего ответить на вопрос, существует или нет в произвольном графе G гамильтонов цикл. Критерии существования, данные в работах Поша [29], ]г[эша-Уильямса [251 и Оре [26], представляют теоретический интерес, но являются слишком общими и не пригодны для произвольных графов, встречающихся на практике (см. задачу 10.1). Алгебраические методы определения гамильтоновых циклов, появившиеся в литературе, не могут быть применены к задачам с более чем несколькими десятками вершин, так как они требуют слишком большого времени работы и большой памяти компьютера. Более приемлемым является способ Робертса и Флореса [30, 31], который не предъявляет чрезмерных требований к памяти компьютера, но время в котором зависит экспоненциально от числа вершин в графе. Однако другой неявный метод перебора [35, 6] имеет для большинства типов графов очень небольшой показатель роста времени вычислений в зависимости от числа вершин. Он может быть использован для нахождения гамильтоновых циклов в очень больших графах. В настоящей главе мы опишем алгебраический метод и два способа перебора.

2.1. Алгебраический метод

Этот метод основан на работе Йоу [37], Даниэльсона [И] и Дхавана [14] и включает в себя построение всех простых цепей с помощью последовательного перемножения матриц.

Внутреннее произведение вершин цени х^, Xg, Хд, . . . . ., Xfi-i, Хи определяется как выражение вида -Хд . . . Хи-\, не содержащее две концевые вершины ) х^ ж х^- Модифицированная матрица смежности В = [р (i, f)] - это {п X ге)-матрица, в которой р (i, /) = Xj, если существует дуга из Xi s Xj ж нуль в противном случае. Предположим теперь, что у нас есть матрица Рг = Pi где pi (i, j) - сумма внутренних произведений

всех простых цепей длины I (li) между вершинами и Xj для Xi Ф Xj. Положим трх (i, i) = О для всех i. Обычное алгебраическое произведение матриц В-Р, = P;+i= \pi+\ (s, t)] определяется как

pi+i{s,t) = Y(f)-Pi(ft), (10.1)

т. е. pi+i (s, t) является суммой внутренних произведений всех цепей из х^ в xt длины 1+1. Так как все цени из х^ в xt, представленные внутренними произведениями из pi (к, t), являются

1) Часто точки между буквами будут опускаться. При к = 2 произведение равно 1.- Прим. ред.

простыми, ТО среди цепей, получающихся из выражения (10.1), не являются простыми лишь те, внутренние произведения которых в pi {к, t) содержат вершину Xg. Таким образом, если из Pi+\{s, t) исключить все слагаемые, содержащие х^ (а это можно сделать простой проверкой), то получим pj+j (s, t). Матрица Pj+j = = (s, t)], все диагональные элементы которой равны О, является тогда матрицей всех простых цепей длины Z + 1.

Вычисляя затем B-Pj+j, находим Р;+2 и т. д., пока не будет построена матрица P -i, дающая все гамильтоновы цепи (имеющие длину п - 1) между всеми парами вершин. Гамильтоновы циклы получаются тогда сразу из цепей в P j и тех дуг из G, которые соединяют начальную и конечную вершины каждой цепи. С другой стороны, гамильтоновы циклы даются членами внутреннего произведения вершин, стоящими в любой диагональной ячейке матрицы В -Pn-i (все диагональные элементы этой матрицы одинаковые).

Очевидно, что в Ka4eoffBe начального значения матрицы Р (т. е. Fj) следует взять матрицу смежности а графа, положив все ее диагональные элементы равными нулю.

а Ь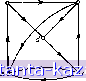

Рис. 10.1. Граф из примера 2.1.1.

2.1.1. Пример. Рассмотрим граф, изображенный на рис. 10.1, матрица смежности которого равна